改进的分级ASLS损失函数：解决不平衡分类问题
104 浏览量
更新于2024-08-27
收藏 746KB PDF 举报
本文探讨了一种针对不平衡分类问题的新型不对称分级最小二乘（Asymmetric Stagewise Least Square, ASLS）损失函数。在传统的stagewise least square (SLS) 损失函数的基础上，ASLS损失函数引入了两个额外参数： ramp系数和margin系数。SLS损失函数的优点，如更好的鲁棒性、计算效率和稀疏性，ASLS进一步扩展了这些特性，通过非对称的阶梯形和边际设计，使其更灵活适应处理数据集中类别分布不均的问题。
在二分类问题中，标准的评估是基于问题相关的损失函数 \( l(f(x), t) \)，其中 \( t \) 是样本 \( x \) 的真实标签，取值为 \( \pm1 \)。然而，在不平衡数据集上，常见的问题是正负类别的样本数量严重失衡，可能导致模型倾向于预测占多数的类别，而忽视少数类别。SLS损失函数在这种情况下可能表现不佳，因为它可能过于关注误差平均，忽略了少数类的重要性。
ASLS损失函数的创新之处在于它能够通过调整这两个新参数来实现对不同类别的差异化处理。ramp系数控制了不同类别样本在训练过程中的学习速率，使得模型能更优先关注少数类；而margin系数则影响了决策边界的设计，确保在保持精度的同时，尽量减少误分类少数类的情况。这种设计使得ASLS损失函数在处理不平衡数据时更加敏感和精确。
此外，文中还提出了一个基于ASLS损失的减维核分类器，该方法仅使用数据集的一部分信息就能生成高效的非线性分类器。这样做的好处在于降低了计算复杂度，同时保持了在不平衡数据集上的良好性能。
实验结果验证了ASLS损失函数在不平衡分类任务中的有效性，它不仅提高了分类精度，而且在处理类别分布严重不均的情况下，能显著改善少数类的识别能力。ASLS损失函数为不平衡数据分类提供了一种有前景的方法，值得进一步研究和应用在实际场景中，如欺诈检测、医疗诊断等领域，以提升模型在实际问题中的鲁棒性和准确性。
An Asymmetric Stagewise Least Square Loss Function for
Imbalanced Classification
Guibiao Xu, Bao-Gang Hu and Jose C. Principe
Abstract— In this paper, we present an asymmetric stagewise
least square (ASLS) loss function for imbalanced classification.
While keeping all the advantages of the stagewise least square
(SLS) loss function, such as, better robustness, computational
efficiency and sparseness, the ASLS loss extends the SLS loss by
adding another two parameters, namely, ramp coefficient and
margin coefficient. Therefore, asymmetric ramps and margins
can be formed which makes the ASLS loss be more flexible and
appropriate for processing class imbalance problems. A reduced
kernel classifier of the ASLS loss is also developed which only
uses a small part of the dataset to generate an efficient nonlinear
classifier. Experimental results confirm the effectiveness of the
ASLS loss in imbalanced classification.
I. INTRODUCTION
I
N this paper, we consider the problem of binary classifi-
cation. In classification, the quality of a classifier 𝑓 (𝒙) is
measured by a problem dependent loss function 𝑙
(
𝑓(𝒙),𝑡
)
,
where 𝑡 ∈{±1} is the true label of pattern 𝒙. 𝑙
(
𝑓(𝒙),𝑡
)
can also be written as 𝑙(𝑧), where 𝑧 = 𝑡𝑓(𝒙) is the margin
variable and can be used to measure the confidence of
classification. Given a training set {(𝒙
𝑖
,𝑡
𝑖
)}
𝑁
𝑖=1
, where each
training pattern 𝒙
𝑖
∈ ℝ
𝑑
, the classifier 𝑓(𝒙) can be found
by empirical risk minimization of 𝑙(𝑧). Misclassification
error rate (0-1 loss) 𝑙
0−1
= ∣∣(−𝑧)
+
∣∣
0
, where (⋅)
+
denotes
the positive part and ∣∣⋅∣∣
0
denotes the 𝐿
0
norm, is the
most appealing loss function for classification because it
relates to the misclassification probability directly. However,
the noncontinuity and nonconvexity of the 0-1 loss make
its optimization NP-hard [1]. Therefore, researchers apply
various convex upper bounds of the 0-1 loss to alleviate this
computational problem [2], such as the hinge loss function
𝑙
ℎ𝑖𝑛𝑔 𝑒
(𝑧)=[(1−𝑧)
+
]
𝑞
(𝑞 =1or2), the logistic loss function
𝑙
𝑙𝑜𝑔
(𝑧) = log[1 + exp(−𝑧)], the least square (LS)loss
function 𝑙
𝑙𝑠
(𝑧)=(1−𝑧)
2
, and the exponential loss function
𝑙
𝑒𝑥𝑝
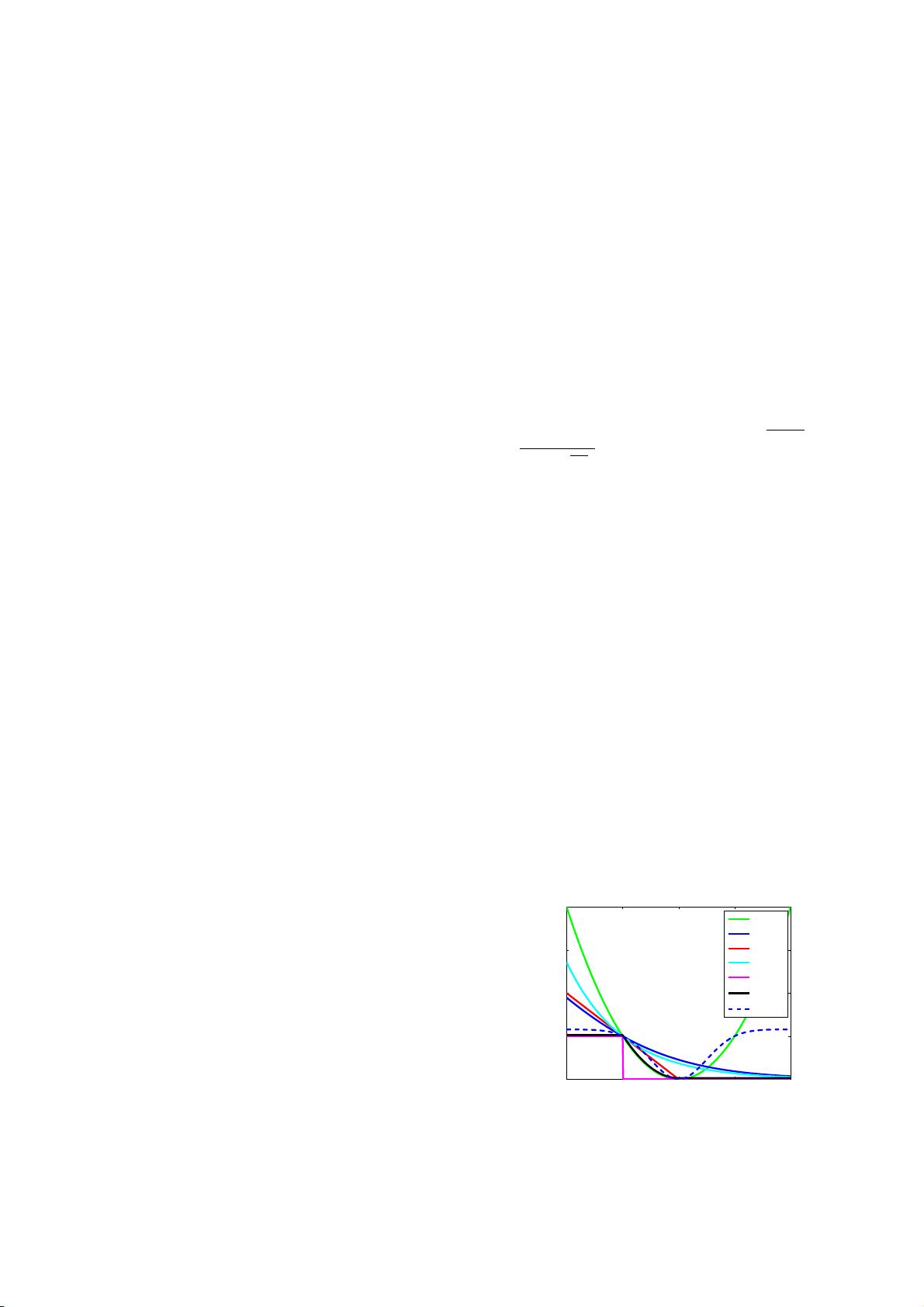
(𝑧) = exp(−𝑧) (see Fig.1). These convex surrogate loss
functions are popular because of their virtues of convex op-
timization like unique optima, abundant convex optimization
tools and theoretic generalization error bound analysis [3].
However, these convex loss functions are poor approximation
to the 0-1 loss and less robust. Despite of the disadvantages
of nonconvex loss functions, various algorithms of noncon-
vex loss functions are studied in [4], [5] which prove that
Guibiao Xu and Bao-Gang Hu are with the NLPR, Institute of Automa-
tion, Chinese Academy of Sciences, Beijing, China (email: {guibiao.xu,
hubg}@nlpr.ia.ac.cn).
Jose C. Principe is with the CNEL, Department of Electrical & Computer
Engineering, University of Florida, Gainesville, FL 32611, USA (email:
principe@cnel.ufl.edu).
This work was supported by NSFC grants #61075051, #61273196 and
China Scholarship Council.
nonconvex loss functions have higher generalization ability,
better scalability and better robustness. The successful appli-
cations of deep neural networks further shows the promising
future of nonconvex loss functions [6]. In [7], Yang and Hu
innovatively proposed a stagewise least square (SLS)loss
function that gradually approximates a nonconvex squared
ramp loss function by adaptively updating the targets (the
details are in Section II-B). SLS loss inherits the advantages
from both convex and nonconvex loss functions. Correntropy
loss function (C-loss) 𝑙
𝐶
(𝑧)=𝛽[1 − exp(−
(1−𝑧)
2
2𝜎
2
)], where
𝛽 =
1
1−exp(−
1
2𝜎
2
)
and 𝜎 is the correntropy window width,
is another nonconvex loss function that was proposed in [8].
One of the appealing advantages of C-loss is that it is more
robust to overfitting compared with other loss functions. Both
the SLS loss and the C-loss are also shown in Fig.1.
Imbalanced classification is another key problem in classi-
fication. Because all the above loss functions assume that the
class distributions and misclassification costs are balanced,
classifiers based on these assumptions tend to classify all
the patterns to be negatives
1
when they run into imbalanced
datasets. The objective of imbalanced classification is trying
our best to separate positives from negatives, and it usually
costs more if we classify positives to be negatives than
otherwise. Hence, a variety of class imbalance learning
methods [9], [10] have been developed which could be
broadly divided into external methods and internal methods
[20], [21]. External methods are about data pre-processing so
as to balance the classes, while internal methods focus on al-
gorithmic modifications in order to reduce their sensitiveness
to class imbalance. MetaCost [11], one-side selection [12]
1
In this paper, we use +1 (positive) to represent the minority class and
-1 (negative) to represent the majority class.
−1 0 1 2 3
0
1
2
3
4
Margin z
Loss
LS
log
hinge
exp
0−1
SLS
*
C−loss
Fig. 1. Loss functions in classification (𝜎 =0.5 for C-loss).
2014 International Joint Conference on Neural Networks (IJCNN)
July 6-11, 2014, Beijing, China
978-1-4799-1484-5/14/$31.00 ©2014 IEEE
1107
下载后可阅读完整内容，剩余7页未读，立即下载
2021-08-07 上传
2022-11-16 上传
2024-11-09 上传
2024-11-09 上传
2024-11-09 上传
2024-11-09 上传
weixin_38553681
- 粉丝: 2
- 资源: 915
我的内容管理
展开
最新资源
- Fisher Iris Setosa数据的主成分分析及可视化- Matlab实现
- 深入理解JavaScript类与面向对象编程
- Argspect-0.0.1版本Python包发布与使用说明
- OpenNetAdmin v09.07.15 PHP项目源码下载
- 掌握Node.js: 构建高性能Web服务器与应用程序
- Matlab矢量绘图工具：polarG函数使用详解
- 实现Vue.js中PDF文件的签名显示功能
- 开源项目PSPSolver：资源约束调度问题求解器库
- 探索vwru系统：大众的虚拟现实招聘平台
- 深入理解cJSON：案例与源文件解析
- 多边形扩展算法在MATLAB中的应用与实现
- 用React类组件创建迷你待办事项列表指南
- Python库setuptools-58.5.3助力高效开发
- fmfiles工具：在MATLAB中查找丢失文件并列出错误
- 老枪二级域名系统PHP源码简易版发布
- 探索DOSGUI开源库：C/C++图形界面开发新篇章
