隐马尔科夫模型：概率建模与应用解析

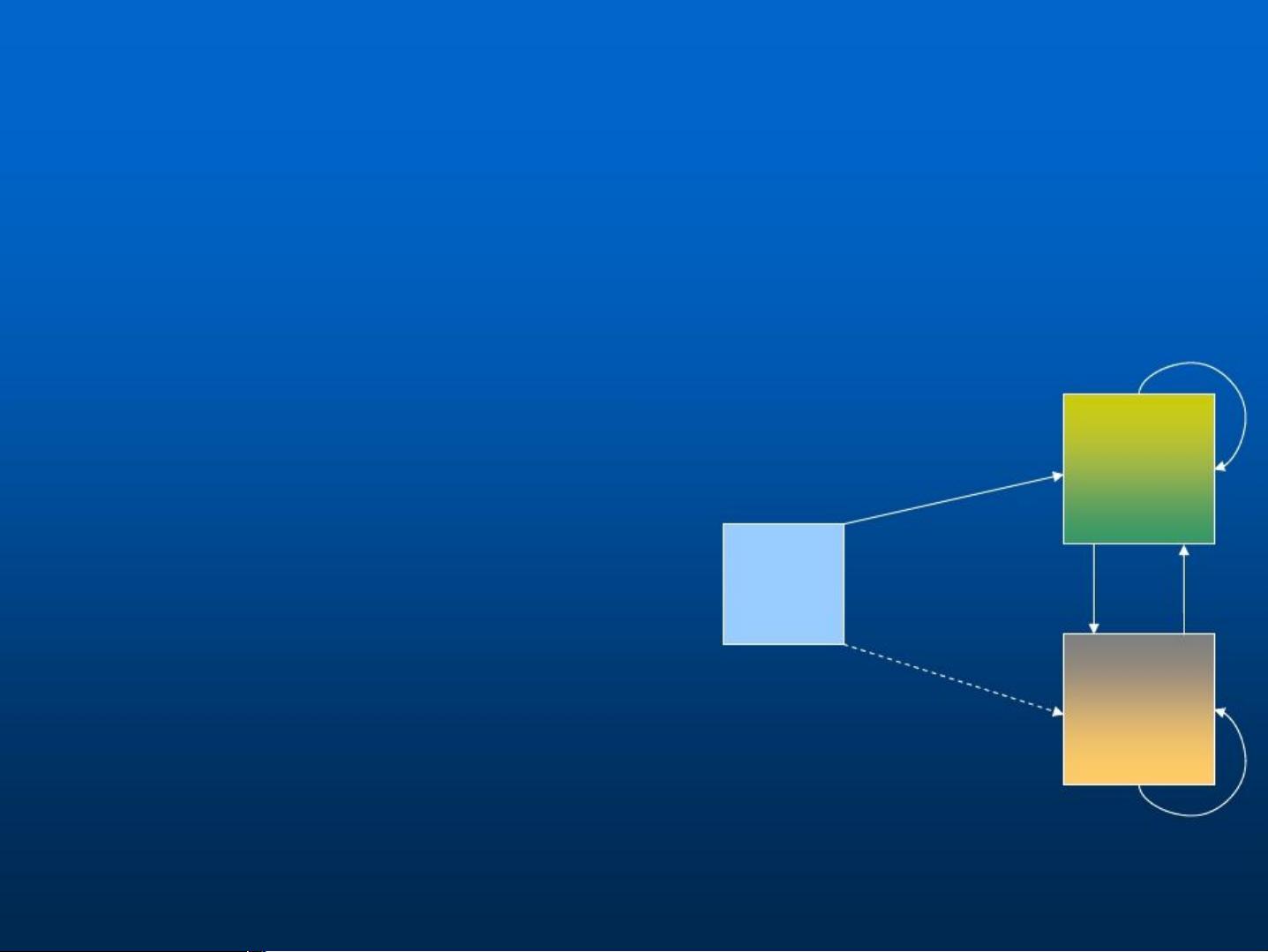
"本文将详细介绍隐马尔科夫模型（HMM）的定义、基本问题以及对应的求解算法。HMM是一种重要的统计建模技术，广泛应用于语音识别、光学字符识别（OCR）以及生物信息学等领域。在生物信息学中，HMM常用于DNA序列分析和基因发现等任务。以下是对HMM的深入解析。 HMM的基本概念 隐马尔科夫模型（Hidden Markov Model，HMM）是一种统计模型，用于处理观察序列与隐藏状态序列之间的关系。在这个模型中，存在一个不可见的随机过程，称为隐藏状态序列，它生成一个可见的随机观测序列。隐藏状态序列对观测序列有直接影响，但观测序列不能直接反映出隐藏状态序列。 HMM的三个基本问题 1. **评估问题（Evaluation Problem）**：给定一个观测序列，计算其由特定HMM生成的概率。在赌场的例子中，这对应于计算给定点数记录出现的概率。 2. **解码问题（Decoding Problem）**：找出最可能生成给定观测序列的隐藏状态序列。在赌场的例子中，我们需要确定哪个点数是由不公平的骰子B掷出的。 3. **学习问题（Learning Problem）**：根据给定的观测序列估计HMM的参数，如隐藏状态的转移概率和观测状态的发射概率。在赌场的例子中，我们要找出作弊骰子和公平骰子掷出各个点数的概率，以及它们何时被使用。 HMM的算法 - **前向算法（Forward Algorithm）**：用于解决评估问题，通过计算观测序列到任意时刻t的累积概率。 - **后向算法（Backward Algorithm）**：与前向算法互补，计算从某个时刻t到序列末尾的累积概率，与前向算法结合可以得到全序列的概率。 - **维特比算法（Viterbi Algorithm）**：用于解决解码问题，找到最有可能生成观测序列的隐藏状态路径。 - **Baum-Welch算法（Baum-Welch Algorithm）**：基于EM（Expectation-Maximization）算法，用于解决学习问题，通过迭代优化HMM的参数。 在赌场示例中，我们可以利用这些算法来解决问题： - 对于评估问题，使用前向算法或后向算法可以计算出给定点数序列出现的概率。 - 解码问题可以通过维特比算法找出最可能的隐藏状态序列，即使用骰子B的点数。 - 学习问题则需要应用Baum-Welch算法，通过观测数据估计骰子A和骰子B的发射概率，以及它们之间的转移概率。 总结，HMM是一种强大的工具，尤其在处理具有隐藏变量的序列数据时。通过理解并应用HMM的这三个基本问题及其对应的算法，我们可以对各种复杂系统进行建模和分析，包括但不限于语言模型、生物序列分析和信号处理等场景。"