鲁棒控制系统：μ分析与综合详解

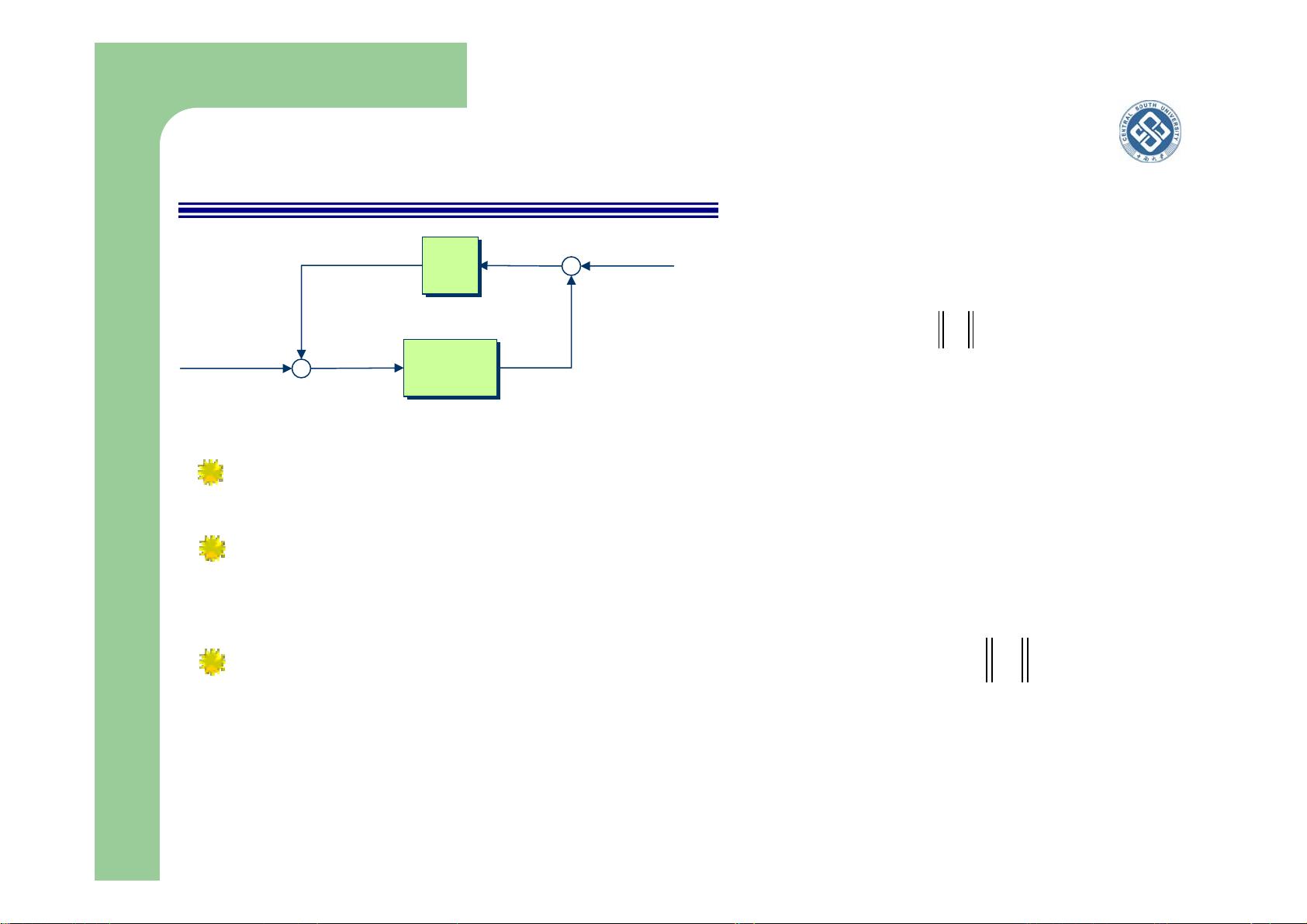
"鲁棒控制系统的μ综合" 鲁棒控制是一种处理系统中存在不确定性因素的控制理论，旨在设计控制器使得系统在各种不确定条件下的性能保持稳定。μ综合是鲁棒控制领域的一个重要方法，用于处理结构不确定性。在这个框架下，我们可以确保控制系统在面对一定范围内的参数变化时仍能保持良好的性能。 1. **μ分析**： μ分析是评估系统鲁棒性能的一种工具，它通过计算μ指标来度量系统对不确定性的容忍程度。μ指标是一个无量纲的数值，其大小反映了系统在不确定性下的稳定性边界。如果μ值小于或等于1，表明系统在所有可能的不确定性下都是稳定的。μ分析不仅考虑了系统的稳定性，还考虑了性能指标，如干扰抑制能力。 2. **鲁棒性分析的一般框架**： 鲁棒性分析通常涉及将系统分解为确定的部分（如控制器K）和不确定的部分（如Δ）。这个框架允许我们分析控制器如何影响整个系统的稳定性。例如，图中的矩阵Δ表示不确定性，而G是系统的基本动态模型。通过分析G和K相互作用后的系统行为，我们可以评估在不确定性的影响下系统的稳定性。 3. **鲁棒性设计问题**： 在鲁棒性设计中，我们需要区分非结构不确定性（如H∞控制和LQG控制处理的类型）和结构不确定性（μ综合主要处理的类型）。非结构不确定性通常涉及到未知但固定的系统参数，而结构不确定性则指的是不确定性具有特定的结构形式。 4. **μ综合**： μ综合是针对结构不确定性的设计方法，其目标是设计控制器K，使得无论不确定性Δ如何变化，系统都能保持内部稳定且μ值小于等于1。这个过程通常涉及线性矩阵不等式（LMIs）的求解，以找到满足鲁棒性能要求的控制器参数。 5. **性能要求**： 在进行鲁棒性分析和设计时，会考虑不同的性能指标，如内部稳定（系统在所有情况下都稳定）、奇异值分析（分析系统对扰动的敏感性）、H∞性能（限制系统对最大扰动的响应）、LQG控制（结合最小化系统输出的二次积分和输入的能量）以及H2性能（衡量系统输出的均方根值）。 6. **不确定性的摄动假设**： 在鲁棒控制中，通常假设不确定性Δ是静态的、有界的，并且可以表示为一个参数矩阵。此外，还会考虑外部输入的影响，如扰动w和输出y，以及它们之间的关系。 通过μ综合，工程师能够设计出不仅能够应对已知不确定性，还能对未知或难以预测的变化保持稳定性的控制器。这种方法在航空、汽车、电力系统等领域有广泛应用，因为这些系统往往面临各种不可预知的环境变化。