常微分方程数值解：欧拉方法与龙格-库塔

"常微分方程数值解法及应用，包括欧拉方法和龙格-库塔方法" 常微分方程在数学、物理、工程等多个领域都有广泛应用，它们描述了动态系统的演化过程。数值解法是处理这类问题的重要手段，尤其是在无法获得解析解或者解析解过于复杂的情况下。本资源主要讨论了一阶常微分方程的初值问题及其数值解法，特别是欧拉方法和龙格-库塔方法。 一、常微分方程的初值问题 初值问题是研究常微分方程的一个核心部分，它涉及到给定初始条件的解的寻找。形式上，一个一阶常微分方程的初值问题可以表示为： \[ \frac{dy}{dx} = f(x, y), \quad y(x_0) = y_0 \] 其中，\( f(x, y) \) 是微分方程的右端项，\( (x_0, y_0) \) 是初始条件。数值解法的目标是找到在某个区间 \( [a, b] \) 内的一系列点 \( x_i \) 和对应的近似解 \( y_i \)，这些点构成的序列能近似地描绘出微分方程的积分曲线。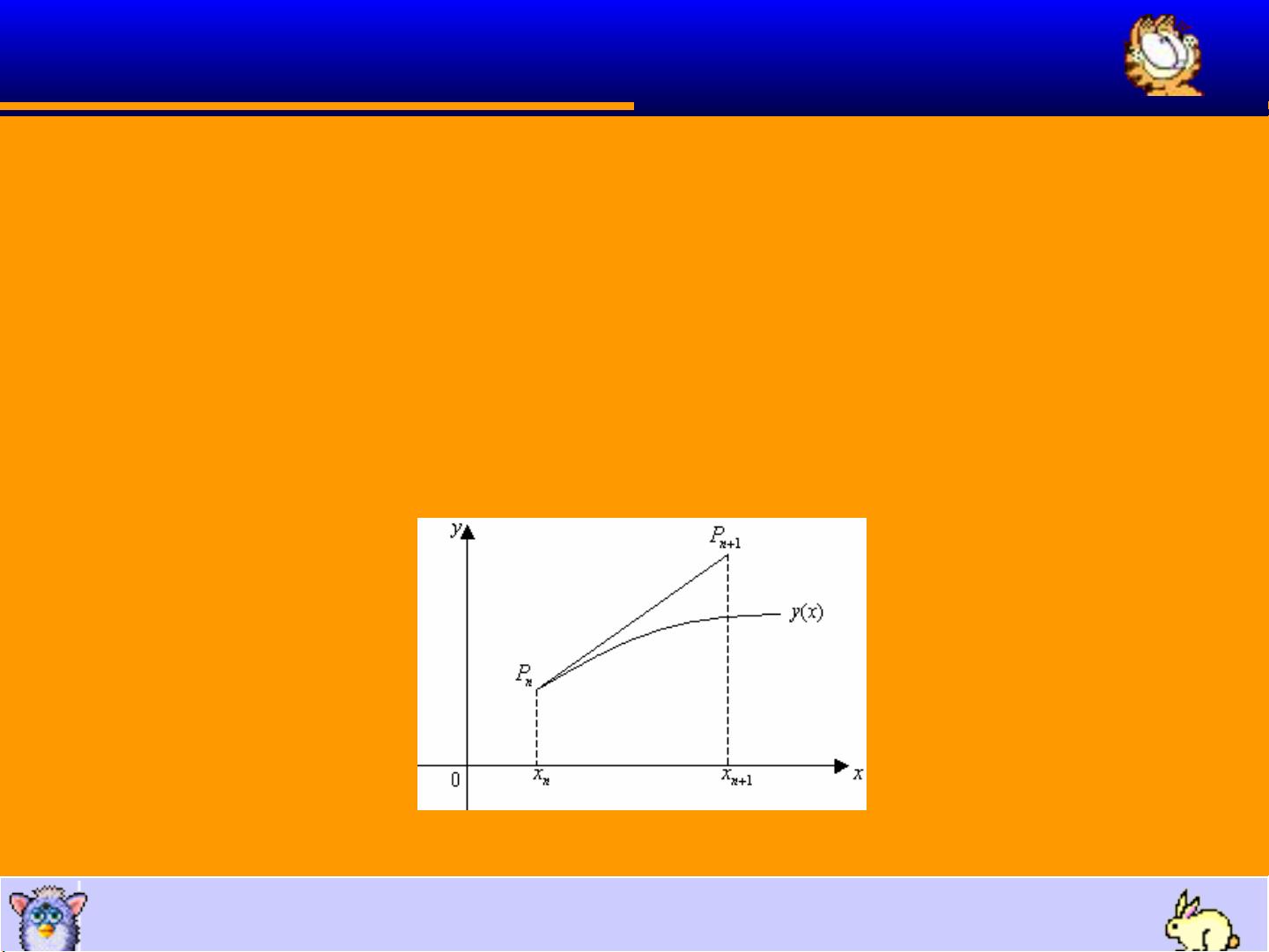 二、欧拉方法 欧拉方法是最简单的常微分方程数值解法之一，由莱昂哈德·欧拉提出。欧拉方法基于微分方程的局部线性化思想，通过连续的步长 \( h \) 将曲线近似为一系列直线段。具体步骤如下： 1. 从初始点 \( (x_0, y_0) \) 开始，根据微分方程的导数 \( f(x, y) \) 计算下一步的方向，即 \( f(x_i, y_i) \)。 2. 沿这个方向前进一个步长 \( h \)，得到新的点 \( (x_{i+1}, y_{i+1}) \)，其中 \( x_{i+1} = x_i + h \)。 3. 近似解 \( y_{i+1} \) 由欧拉公式给出： \[ y_{i+1} = y_i + h \cdot f(x_i, y_i) \] 欧拉方法虽然简单直观，但其精度较低，特别是在步长 \( h \) 较大时，容易导致较大的误差。 三、龙格-库塔方法 为了提高精度，人们发展出了更复杂的数值解法，其中最著名的是龙格-库塔方法。龙格-库塔方法是一类广义的欧拉方法，它通过考虑多个中间点的导数来改进近似。例如，四阶龙格-库塔方法（也称为经典四阶龙格-库塔方法）会利用四个不同的中间点来计算下一个步长的近似值，从而获得更高的精度。 在MATLAB中实现欧拉方法或龙格-库塔方法通常涉及以下步骤： 1. 定义微分方程的函数 \( f(x, y) \)。 2. 设置初始值、结束值、步长和迭代次数。 3. 使用循环结构进行迭代，每次迭代中应用相应的数值解法更新解。 4. 存储并返回每个时间步的解。 通过适当的编程，这些数值解法可以被用于模拟各种实际问题，如物理系统的运动、生物系统的动力学模型等。然而，选择合适的步长 \( h \) 对于控制误差和计算效率至关重要，通常需要通过实验或误差分析来确定。同时，对于高阶微分方程或带有边界条件的问题，可能需要采用更复杂的数值方法，如隐式方法或有限差分法。