计算理论考试：图灵机、语言类及判定问题解析

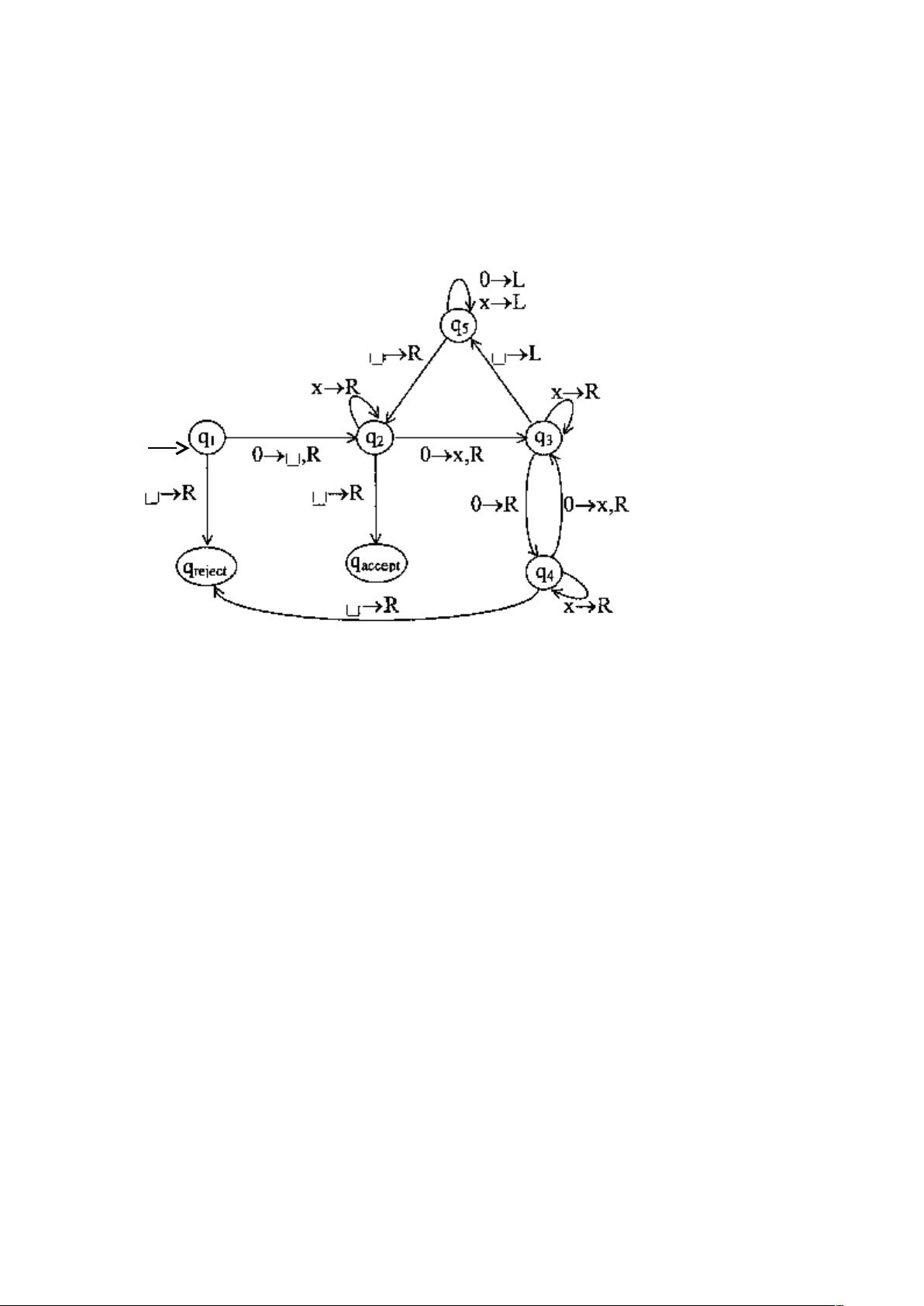
本资源是一份关于计算理论的考试试题，涵盖了北京理工大学2002-2003学年第一学期研究生的计算理论课程内容。首先，题目涉及了图灵机的基本概念和应用，包括状态集、输入字母表、工作字母表和起始状态的设定。对于一个特定的图灵机M，问题要求分析其状态转移和处理输入0000的能力，并通过正则语言的泵引理来判断语言A={0^2n | n > 0}是否为正则语言，结果表明该语言是非正则的。 接下来，题目探讨了多带和单带确定型图灵机的区别以及它们识别的语言类别。多带确定图灵机能够识别图灵可识别语言，而且时间复杂性上，多带图灵机可以转化为单带图灵机，但时间复杂度有所提升。非确定图灵机同样识别图灵可识别语言，但非确定性使得时间复杂性的增长更为明显。 第三部分涉及自动机理论，具体是证明ATM（接受图灵机集合）与ETM（存在图灵机集合）的关系，通过构造函数f将ATM中的机器映射到ETM的补集，从而证明了两个集合之间的包含关系。 最后，题目关注的是图论语言A={<G>|G是连通无向图>，要求证明语言A的可判定性和多项式时间可判定性。通过设计一个图灵机T，它可以通过标记法遍历图的节点并检查连通性，从而实现判定任务。这展示了如何利用计算理论工具来处理图形结构的问题。 总结来说，这份试题深入考查了计算理论的基础概念，如图灵机、正则语言、图灵机的时间复杂性和图论，以及这些理论在实际问题中的应用。对于理解计算理论的复杂性理论和语言表示能力具有较高的参考价值。