二分图匹配与匈牙利算法解析

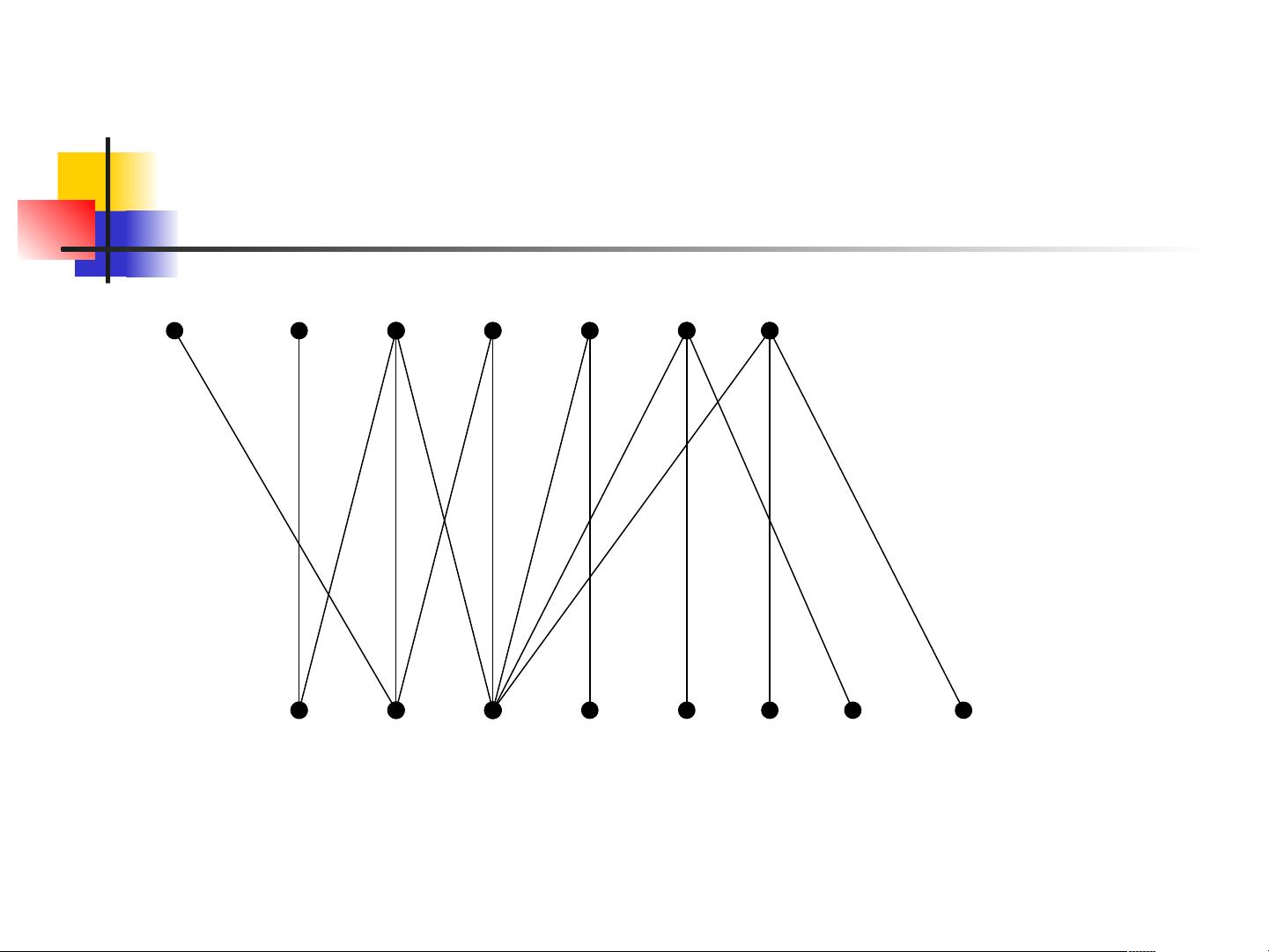
"HDU二分匹配及其应用" 在ACM程序设计领域，二分匹配是一种重要的图论概念，尤其在解决实际问题时有着广泛的应用。本资料由杭州电子科技大学的刘春英老师提供，旨在帮助编程爱好者，尤其是ACMer更好地理解和运用二分匹配。 二分图，又称为两色图，是指一个图的顶点可以被分成两个不相交的集合X和Y，所有的边都连接不同集合中的顶点。例如，婚配问题就是一个经典的二分图模型，其中男性和女性分别构成两个集合，边代表可能的匹配关系。 二分图的最大匹配问题是寻找二分图中最多的一对顶点，使得每对顶点间有一条边相连，且没有两条边共享同一个顶点。这个问题在很多实际场景中都有应用，如分配任务、分配资源等。 求解二分图最大匹配的常用算法是匈牙利算法，它基于Hall定理。Hall定理指出，二分图存在完美匹配（即每个顶点都被匹配）的充分必要条件是：对于任何集合A，与A邻接的顶点集合T(A)的大小至少等于A的大小。简单来说，如果任一子集的邻接点数都不小于子集的大小，那么存在一个满足所有顶点的匹配。 匈牙利算法的基本步骤包括： 1. 初始化一个匹配M。 2. 如果所有顶点都已经匹配（X集合饱和），则结束。 3. 否则，找一个未匹配的顶点x0，并初始化两个集合V1和V2。 4. 如果T(V1)等于V2，表示无法找到匹配，停止。 5. 否则，找一条从x0到未匹配顶点y的可增广路径P，更新匹配M。 6. 如果y已饱和，找到与y相邻的已匹配顶点z，扩展V1和V2，然后回到步骤4。 通过不断寻找并利用可增广路径，匈牙利算法能够确保找到二分图的最大匹配。在实际操作中，通常会用DFS或BFS来寻找这样的路径。 此外，二分图的最大匹配问题还可以引申出其他相关问题，如最小顶点覆盖、最小路径覆盖和最大独立集。最小顶点覆盖是在二分图中找到最少数量的顶点，使得它们覆盖所有的边；最小路径覆盖是寻找图中最小数量的不相交路径，使得所有顶点都被路径包含；最大独立集是在二分图中找到最大数量的不相邻顶点。 二分匹配的概念和匈牙利算法在解决实际问题时具有很高的实用价值，例如在婚姻匹配、作业分配、网络调度等领域都有所应用。因此，掌握这些知识对于ACMer和IT专业人士来说至关重要。