工科生实用指南：从小波变换到窗口傅里叶变换

"工科生眼中的小波变换" 小波变换是工科领域中一种重要的数学工具，尤其在信号处理和图像分析中有着广泛应用。它为理解和解析非平稳信号提供了强大的理论基础。小波分析源自傅里叶变换，但弥补了傅里叶变换在时频分辨率上的不足。 1、概述 小波变换是傅里叶变换的一种扩展，它能够同时提供时间域和频率域的信息，从而在时间和频率上具有局部特性。与传统的傅里叶变换相比，小波变换可以在不同的尺度和位置上对信号进行分析，这对于检测信号的突变和局部特征非常有用。 2、变换的意义 小波变换的核心价值在于其时频局部化特性。在许多实际应用中，如医学诊断、声音分析、图像处理等，信号往往包含瞬态信息，这些信息在时域和频域中同时存在。小波变换可以揭示这些隐藏的特征，使我们能够更准确地理解和解释数据。例如，脑电图（EEG）的分析，原始的时域信号难以直接解析，通过小波变换可以揭示不同频率成分，有助于诊断脑部疾病。 3、从傅里叶变换到窗口傅里叶变换 傅里叶变换虽能提供全局频率信息，但它不能很好地定位信号的时间信息。为了解决这个问题，引入了窗口傅里叶变换。窗口函数的应用使得傅里叶变换能在有限的时间区间内进行，从而提高了时频分辨率。然而，窗口傅里叶变换仍无法同时得到精确的时间和频率信息，这时小波变换应运而生，它采用可变宽度的“窗口”（小波基），实现了真正的时频局部分析。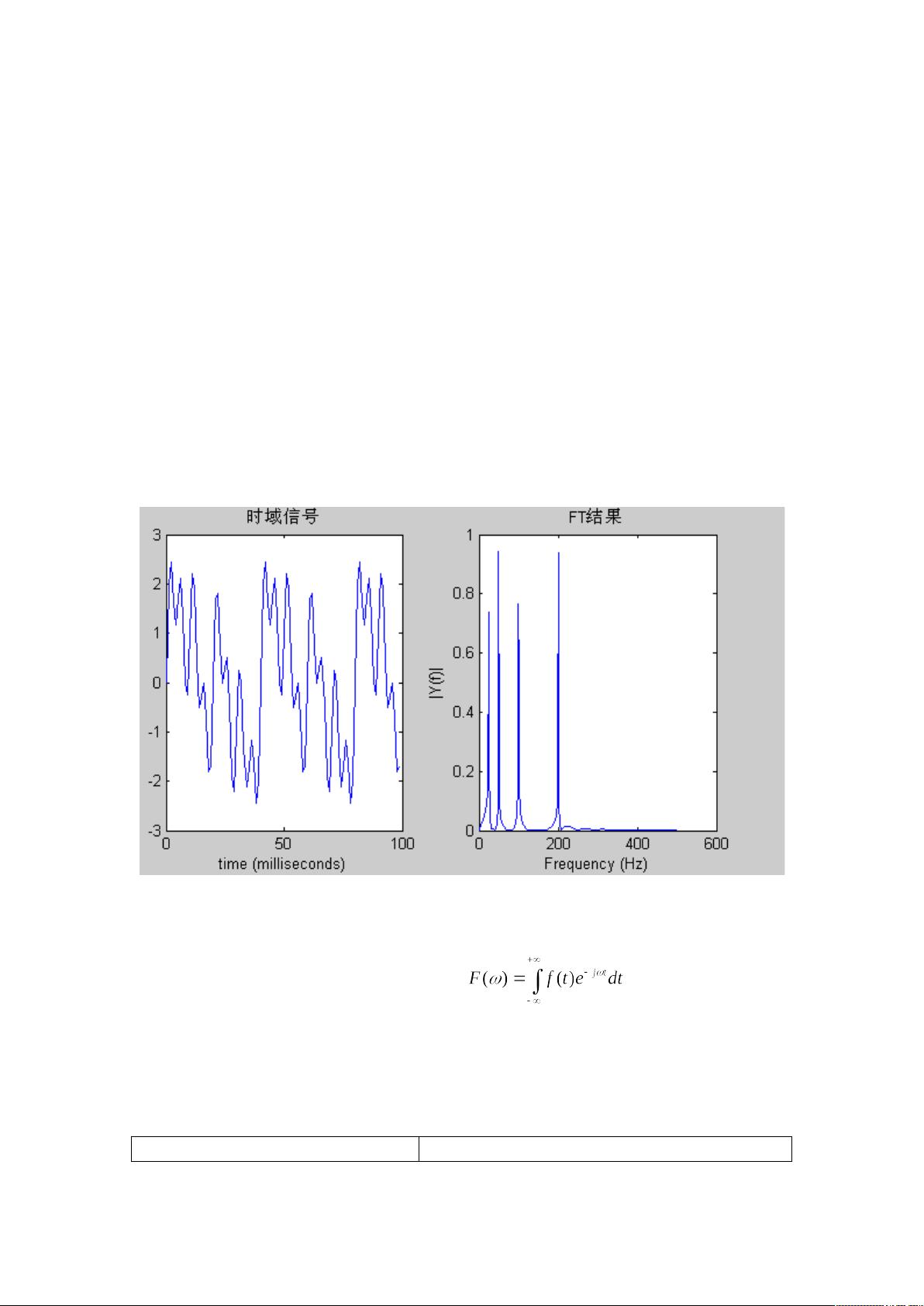 3.1傅里叶变换 傅里叶变换是一种将信号从时域表示转换为频域表示的方法，它假设信号是周期性的或近似周期性的。1822年，傅里叶提出了这一理论，它在物理学、工程学等领域有着广泛的应用。 3.2窗口傅里叶变换 窗口傅里叶变换是傅里叶变换的改进，通过在傅里叶变换前乘以一个窗口函数，限制了分析的频率范围，但牺牲了连续性，导致了时频分辨率的妥协。 3.2.1直观认识 窗口函数限制了分析的频率范围，使得变换结果只反映窗口内的信号特性，但会导致频谱泄漏和分辨率下降。 3.2.2窗口傅里叶变换中的时频窗 时频窗是窗口傅里叶变换的关键，不同的窗口形状会影响分析结果的时频分辨率。小波变换可以看作是一种自适应的时频窗，它允许窗口大小随时间变化，从而提供更好的时频分辨率。 4、小波变换 4.1连续小波变换定义 连续小波变换是小波分析的基础，它通过调整小波基函数的位置和缩放来适应不同时间和频率的信息。 4.2小波基的自适应时频窗及其度量 小波基函数的选择直接影响到小波变换的效果。理想的基函数应该满足正交性、归一化和局部化等条件，能够有效地刻画信号的时频分布。 5、小结 小波变换提供了一种有效的时频分析手段，不仅具备傅里叶变换的频域分析能力，还能捕捉到信号的动态变化。对于工科生来说，理解小波变换的实用性和物理意义比深入复杂的数学理论更为重要。通过学习小波变换，可以掌握一种更强大的信号分析工具，从而解决更多实际问题。