DAI et al.: ANALYTICAL MODELING OF RESOURCE ALLOCATION IN D2D OVERLAYING MULTIHOP MULTICHANNEL UPLINK CELLULAR 6635
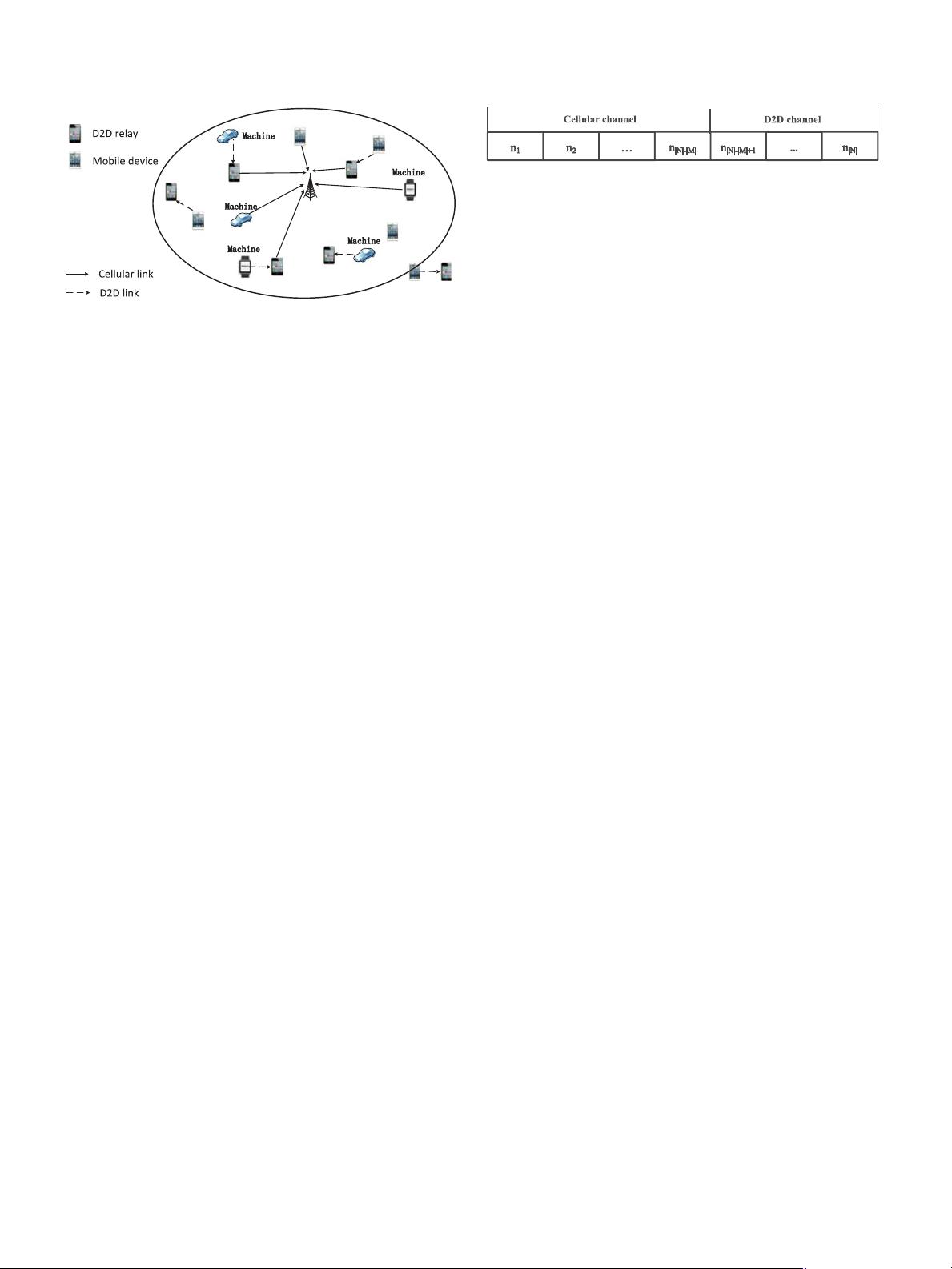
Fig. 1. Cellular network with cellular users and D2D users, where the solid
line denotes the cellular link, and the dashed line denotes the D2D link.
larger than a threshold; otherwise, the transmission goes into
outage.
III. S
YSTEM MODEL
A. Network Model
We consider a multi-channel D2D-enabled single-tier uplink
cellular network in which a mobile device or a machine can com-
municate with the BS directly or send data to its intended relay
as shown in Fig. 1. Different from existing works, the cellular
network consists of multiple BSs, cellular users and D2D users
with their own D2D relays. Specifically, a tagged D2D user can
only upload data to its paired D2D relay and then the D2D relay
sends data to the nearest BS. As for a tagged cellular user, it can
upload the data to the nearest BS directly. Obviously, cellular
users upload data to BSs in one hop and D2D users upload data
to BSs in two hops. What’s more, D2D users and D2D relays
adopt the bipolar model [25]. That is, D2D users are assumed to
have D2D relays with a fixed distance l
d
. This model provides
a deep insight into how the network performance (coverage
probability and ergodic rate) changes with the distance. In the
following sections, we call the transmissions between D2D users
and D2D relays as D2D transmissions and that between cellular
transmitters (D2D relays and cellular users) and BSs as cellular
transmissions.
We model the locations of BSs (resp. cellular users and D2D
users) by realization of Poisson point process, to guarantee these
BSs (resp. cellular users and D2D users) are uniformly and
independently located on the plane. In what follows, we assume
the BSs are spatially distributed according to the PPP Φ
b
=
{x
1
,x
2
, ..., x
i
, ...} of density λ
b
, where x
i
is the location of
the ith BS. We denote by Φ
c
= {y
1
,y
2
, ..., y
i
, ...} and Φ
d
=
{z
1
,z
2
, ..., z
i
, ...} the sets of cellular users’ locations and D2D
users’ locations, respectively, and we suppose Φ
c
and Φ
d
to be
some realization of independent homogeneous PPPs of densities
λ
c
and λ
d
.
B. Channel Model
In order to mitigate the interference during the transmis-
sions in the network, we select overlay mode in this pa-
per. The total available bandwidth is divided into a set of
Fig. 2. Spectrum allocation for cellular transmissions and D2D transmissions.
orthogonal channels N = {n
1
,n
2
, ..., n
|N |
}, where |N | de-
notes the number of channels. Furthermore, the set of chan-
nels N is partitioned into two disjoint subsets of channels
N
c
and N
d
, which is described in Fig. 2. Specifically, the
channels set N
d
= {n
|N |−|M |+1
,n
|N |−|M |+2
, ..., n
|N |
} (|M| <
|N|) is allocated just for D2D transmissions. The other set
N
c
= {n
1
,n
2
, ..., n
|N |−|M |
} is allocated for cellular transmis-
sions. Therefore, for the D2D transmission at a D2D user
in channel n
i
, |N|−|M| <i≤|N|, it will be interfered
only by surrounding D2D users which transmit to their own
D2D relays operating on the same channel. As f or a cellu-
lar transmitter, the interference comes from the cellular trans-
mitters which upload data to the BSs in the same channel.
In this paper, we assume each transmitter, whether a D2D
user or a D2D relay or a cellular user, needs one channel for
transmission.
If the number of cellular users and D2D relays is much greater
than that of cellular channels, some users or relays may have
no chance to obtain a channel for data transmission. To avoid
this situation, the hybrid access mechanism for cellular trans-
missions operates as follows.
1) When the number of cellular transmitters associating with
a tagged BS is no greater than the number of cellular
channels, the BS assigns a unique channel from N
c
to
each of its cellular transmitters randomly.
2) When there are more than |N|−|M| cellular transmitters
uploading data to a BS, they are served by channel-sharing
with equal time proportion.
Channel-sharing with equal time proportion [26] is a method
to allow all the cellular transmitters to upload data to the BSs.
For example, when the total number of associated cellular trans-
mitters (n
u
) is greater than that of cellular channels (n
c
), all the
cellular transmitters can upload data to the BSs through cellular
channels, but the time occupation is changed to n
c
/n
u
.Asfor
the channel assignment of D2D transmissions, each D2D pair
selects a channel randomly from channel set N
d
.
We denote by P(x, y) the power received at a point y from
a transmitter located at point x. As adopting the general power-
law propagation model to characterize the path-loss effect of
transmissions, the received power is given by P (x, y)=P
x
·
h
x
y
· l(x, y), where
1) P
x
is the transmit power from point x;
2) h
x
y
represents the channel gain between x and y;
3) l(x, y)=r(x, y)
−α
denotes the path-loss between x and
y, with α>2 is the path-loss exponent.
Moreover, h
c
(resp. h
d
) is used to represent the channel
gains in cellular transmissions (resp. D2D transmissions). α
c
and α
d
are the path-loss exponents for the cellular trans-
missions and D2D transmissions, respectively. All the chan-
nel gains, h
c
and h
d
, are assumed to be i.i.d and ex-
ponentially distributed with mean μ
c
and μ
d
, respectively.









