线性回归模型：OLS估计与拟合优度解析

"估计方程-线性回归模型" 线性回归是一种统计分析方法，用于研究两个或多个变量之间的关系，特别是连续响应变量与一个或多个连续或分类预测变量之间的关系。在这个模型中，我们通常关注简单线性回归，这是一种最基本的线性回归形式，涉及到一个响应变量（通常表示为y）和一个预测变量（表示为x）。简单线性回归模型可以数学地表示为： \[ y = \beta_0 + \beta_1 x + u \] 其中，\( \beta_0 \) 是截距，\( \beta_1 \) 是斜率，\( u \) 是误差项或随机扰动项。 在进行线性回归分析时，有几个重要的假定需要满足： 1. 线性于参数：模型的形式是线性的，即响应变量与预测变量之间的关系是线性的。 2. 随机抽样：样本是从总体中随机抽取的，保证了样本的代表性。 3. 解释变量的样本有变异性：预测变量在样本中不是常数，有变化性。 4. 零条件均值：误差项的期望值为0，即 \( E(u|x) = E(u) = 0 \)，这意味着预测变量对误差项没有系统性影响。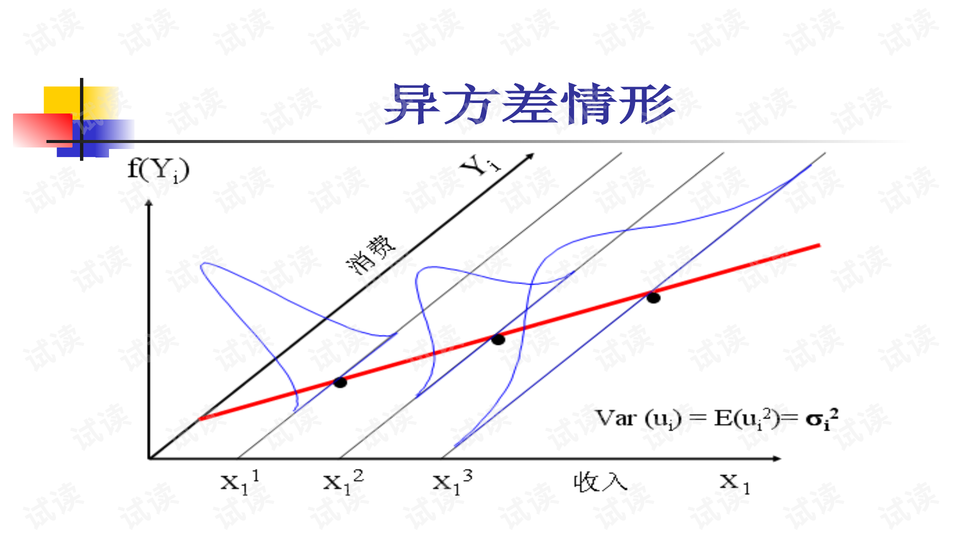 5. 同方差性：误差项的方差在所有水平的预测变量上是恒定的，即 \( Var(u|x) = \sigma^2 \)。 估计线性回归模型参数的过程称为最小二乘法（Ordinary Least Squares, OLS），目标是找到最佳的 \( \beta_0 \) 和 \( \beta_1 \) 的值，使得预测值与实际观测值之间的差异（误差）最小。通过解决以下估计方程来找到斜率的估计值 \( \hat{\beta}_1 \)： \[ \sum_{i=1}^{n}(y_i - (\hat{\beta}_0 + \hat{\beta}_1 x_i))^2 \] 最小化这个误差平方和可以得到参数的估计值 \( \hat{\beta}_0 \) 和 \( \hat{\beta}_1 \)。 线性回归的拟合优度（R²）是衡量模型解释数据变异程度的一个重要指标，它表示因变量的总变异中被模型解释的比例。R²的计算公式如下： \[ R^2 = 1 - \frac{SSR}{SST} \] 其中，SST是总平方和，SSE是解释平方和，SSR是残差平方和。R²的值范围在0到1之间，值越接近1，表示模型对数据的拟合程度越高。 误差项的概率分布对于线性回归的统计推断至关重要。在最小二乘估计中，只要误差项的方差存在且与解释变量无关，OLS估计量就是最佳线性无偏估计量（BLUE）。然而，为了进行区间估计和假设检验，通常需要对误差项的分布作出额外的假定，比如正态性假定，即误差项 \( u \) 遵循正态分布，其均值为0，方差为 \( \sigma^2 \)，且误差项之间无协方差。这种假定被称为经典正态线性回归假定，是许多统计推断方法（如t检验和F检验）的基础。如果这些假定不成立，可能会影响结果的解释和推断。