向量基础：游戏开发中的关键概念

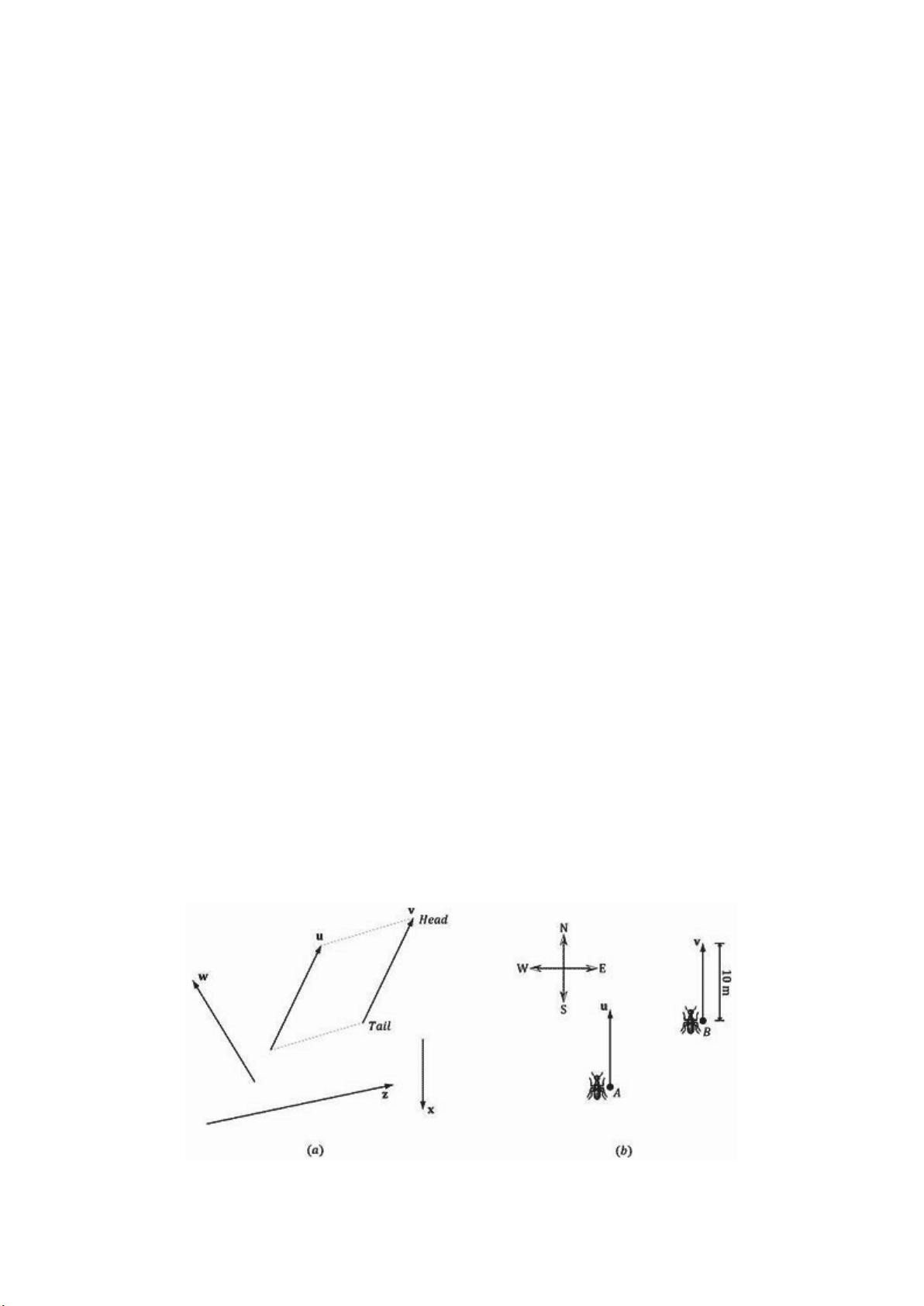
"1.1向量1 - 介绍向量的概念、运算及其在3D游戏开发中的应用，强调XNA数学中的向量函数和向量类的理解，以及向量的几何表示和等价条件" 向量是计算机图形学、游戏开发、物理模拟等领域不可或缺的基础概念。它不仅包含了大小，还具有方向，这使得向量能够描述力、位移、速度等物理量。在几何上，向量通常用有向线段表示，长度代表大小，箭头指示方向，而位置的改变并不影响向量的本质。 学习向量时，首先要理解其基本性质：两个向量相等当且仅当它们的分量完全相同，即长度相等且方向一致。这意味着即使向量在空间中的位置不同，只要它们的大小和方向相同，那么这两个向量就是等价的。例如，在图1.1a中，向量u和v因具有相同的长度和方向而相等。 在3D游戏中，向量可以用来表示玩家的视角方向、物体的运动轨迹、光照的方向等。理解向量的运算是非常关键的，比如向量的加法允许我们将多个力或位移合并，向量的减法则可以表示相对位移。此外，向量乘以标量（ scalar）可改变其大小，而向量点积和叉积则涉及几何特性，如平行、垂直和面积。 XNA数学库提供了丰富的向量函数和类，帮助开发者进行向量操作，如计算两个向量的夹角、找到单位向量、确定向量的投影等。熟悉这些函数和类能显著提高编程效率，并确保计算的准确性。 在坐标系中，向量可以用一组坐标值表示，例如在2D平面上，向量可以用(x, y)来描述；在3D空间中，向量则由(x, y, z)三组分量构成。这种表示方法便于进行数学运算，并且在处理3D游戏中的位置和方向时特别有用。例如，向量的加法简单地将对应坐标的值相加，而向量与标量的乘法则是每个分量分别乘以标量。 掌握向量的理论知识和实际应用是游戏开发和3D图形编程的基础。通过学习向量的表示、运算和几何意义，开发者能够更好地理解和实现游戏中的物理效果、碰撞检测和动画系统，从而提升游戏的真实感和玩家体验。