小波变换与多分辨率处理详解：从入门到精通

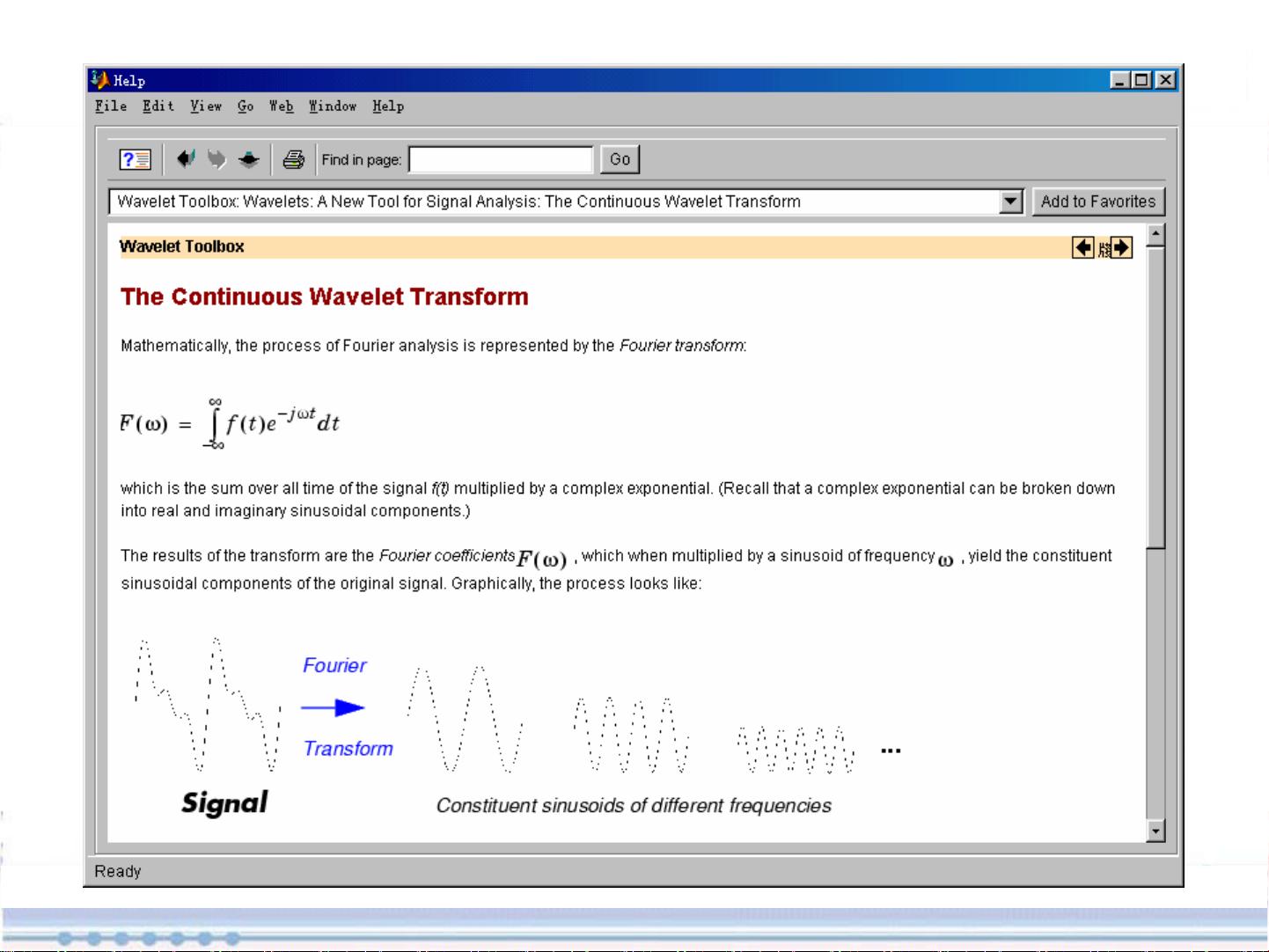
小波变换和多分辨率处理是一门深入理解信号处理和数学分析的重要领域。本资源提供了全面的介绍，从预备知识开始，引导读者逐步掌握这个领域的核心概念。 1. **预备知识** - 首先，读者需要了解L2(R)空间，这是小波理论的基础，它是所有能量有限函数的集合，其正交分解和变换是构建小波理论的关键。这里提到的标准正交基gi(t)使得任何函数f(t)可以表示为它们的线性组合。 2. **Fourier变换与信号时频局部化分析** - Fourier变换是传统的时间域信号分析工具，但小波变换则能提供更精细的时频分析能力。小波分析能实现信号的局部化特性，克服了傅立叶变换全局频率分析的局限。 3. **连续与离散小波变换** - 连续小波变换适用于信号的连续分析，而离散（二进）小波变换则是将连续理论应用到数字信号处理中的重要步骤，例如Mallat算法就是一种高效的离散小波变换方法。 4. **多分辨率分析** - 在L2(R)中进行多分辨率分析，意味着将信号分解为不同尺度和频率的信息，这有助于提取信号的不同特征，如高频细节和低频成分。 5. **二维小波变换** - 对于二维图像信号，需要扩展到二维小波变换，这不仅考虑了空间维度，还能保持时频局部化的优点，常用于图像处理中的去噪、压缩和特征提取。 6. **标准正交小波基的构造** - 构造适合特定应用场景的小波基至关重要，标准正交小波基的选择直接影响信号的重构质量和分析效果。 7. **常用小波函数** - 了解并熟悉一些常见的小波函数，如Haar小波、Daubechies小波等，这些函数各有特点，适用于不同的信号处理任务。 通过这一系列讲解，读者可以从基础的傅立叶分析出发，逐步深入小波变换的世界，掌握多分辨率分析的方法，以及如何运用小波处理实际信号，如图像数据。这对于初学者来说，是一份既适合入门又便于进阶的宝贵资料。