MATLAB中的数值计算：三角与双曲函数解析

"本章介绍了数值计算与数据分析中的基本数学函数，包括三角函数与双曲函数，如sin、sinh、cos、cosh、tan、tanh、cot、coth等，强调了在计算过程中浮点精度的影响以及相关函数的使用格式和示例。" 在数值计算与数据分析中，掌握基本的数学函数是至关重要的。本章首先提到了正弦函数`sin`和双曲正弦函数`sinh`。`sin(X)`用于计算参数X中每个角度分量的正弦值，角度单位为弧度。需要注意的是，由于计算机中pi是π的浮点近似值，因此`sin(pi)`并不严格等于零，而是非常接近零的一个值，即浮点精度相关的无穷小量eps。同样地，`sinh(X)`用于计算双曲正弦值。 接着，章节介绍了余弦函数`cos`和双曲余弦函数`cosh`。`cos(X)`计算X的每个角度分量的余弦值，同样，`cos(pi/2)`并不等于精确的零。`cosh(X)`则用于求解双曲余弦函数值。 接下来是正切函数`tan`和双曲正切函数`tanh`。`tan(X)`计算弧度制下的正切值，而`tanh(X)`则计算双曲正切值。值得注意的是，`tan(pi/2)`在数学上未定义，但在计算机中会得到一个与浮点精度相关的无穷小量。 此外，章节还提到了余切函数`cot`和双曲余切函数`coth`。`cot(X)`计算弧度制下的余切值，`coth(X)`计算双曲余切值。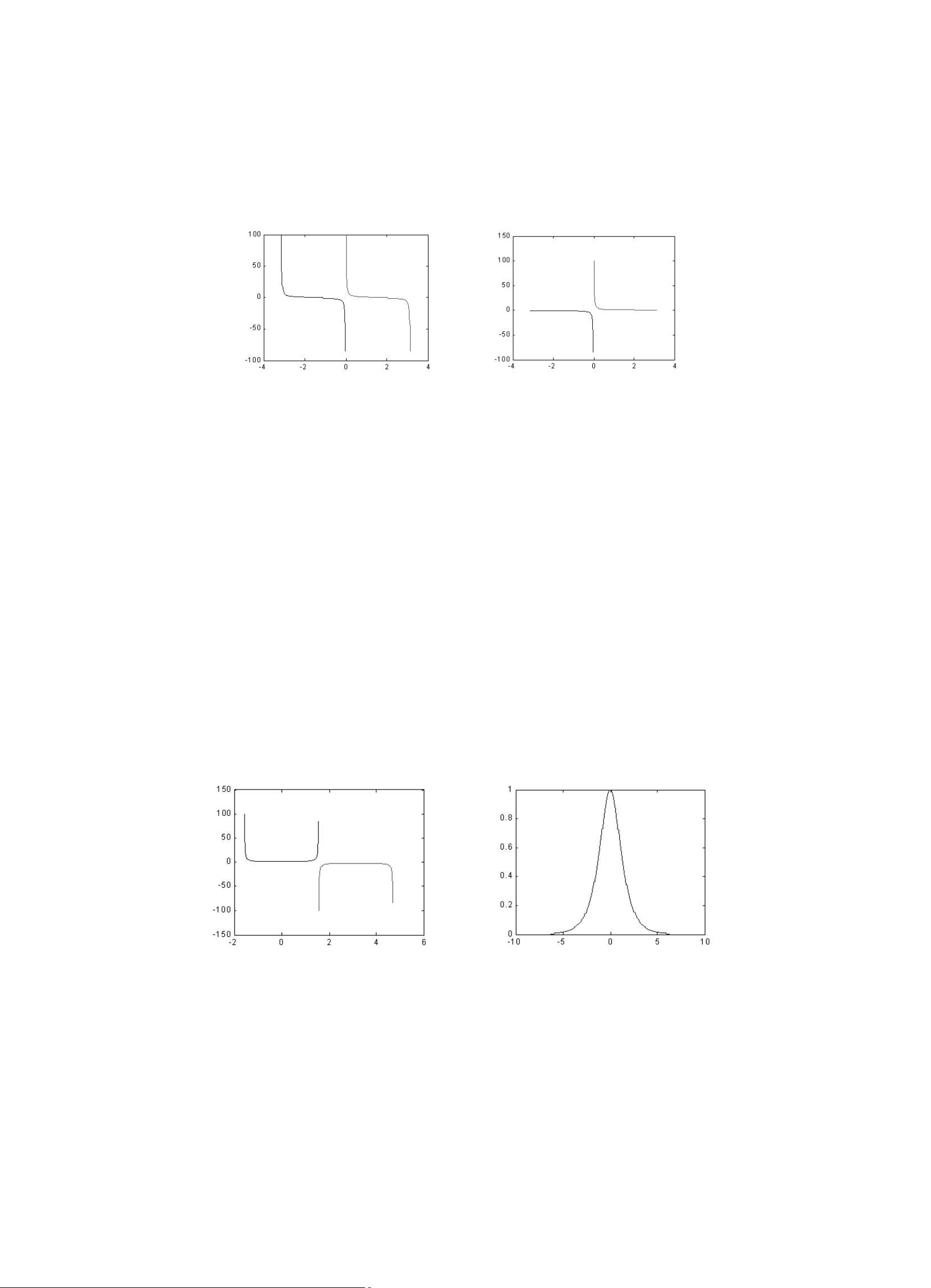 为了更好地理解这些函数，书中给出了多个示例，通过绘制函数图形帮助读者直观感受各函数的特性。例如，例2-1展示了正弦函数`sin(x)`和双曲正弦函数`sinh(x)`的图形，例2-2展示了余弦函数`cos(x)`和双曲余弦函数`cosh(x)`的图形，例2-3展示了正切函数`tan(x)`和双曲正切函数`tanh(x)`的图形，而例2-4则涉及余切函数`cot(x)`和双曲余切函数`coth(x)`的图形。这些图形对于理解和应用这些函数非常有帮助，尤其是在处理复杂数值计算和数据分析任务时。 在实际的编程和计算中，了解这些基本函数的行为和限制，尤其是它们在接近某些特定点（如`pi/2`或`pi`）时的表现，能够避免误差并优化计算效率。掌握这些基础知识是进行高效数值计算和数据分析的前提。