探索栈的多样出栈顺序：n个操作数序列的输出序列总数

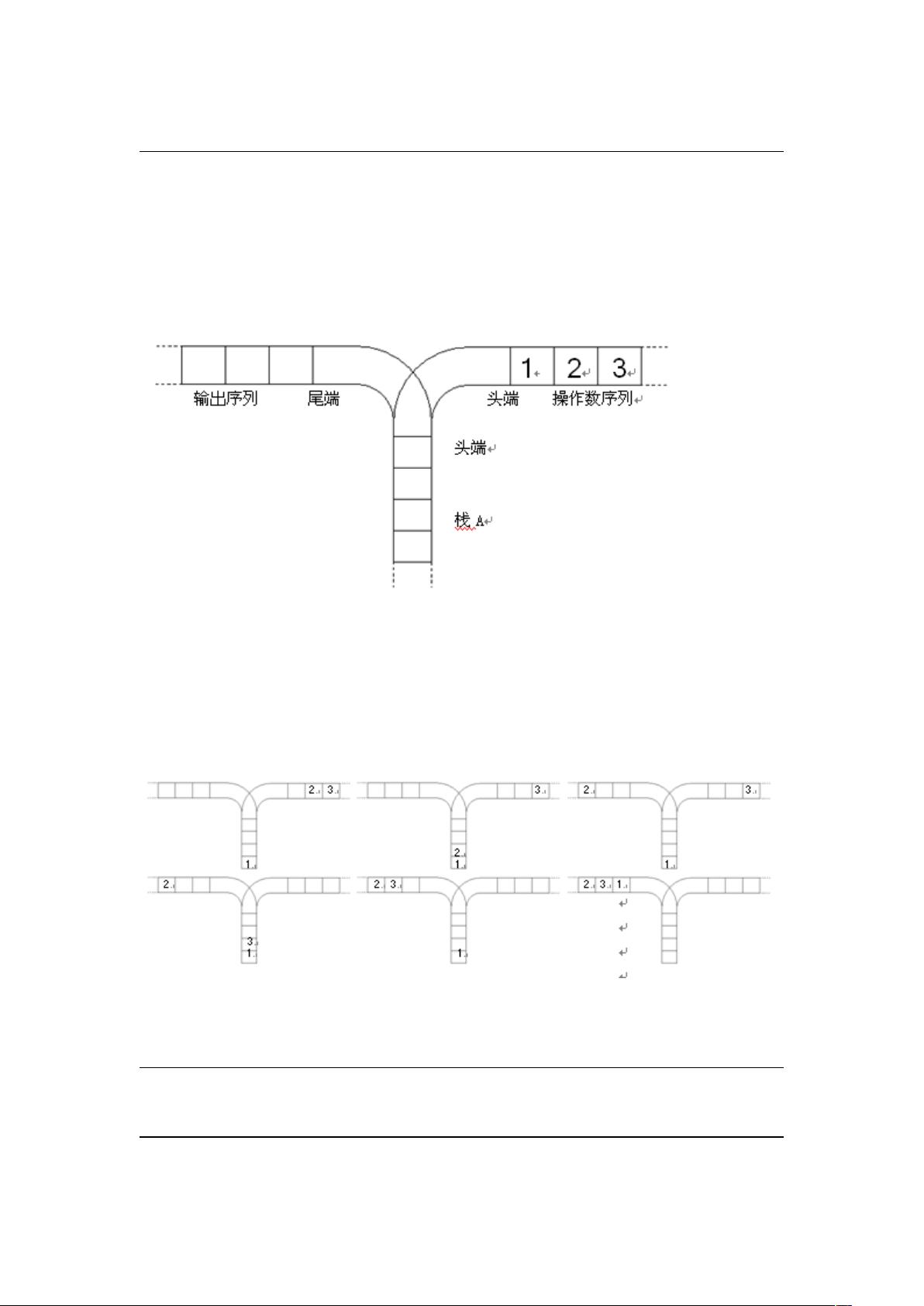
栈的出栈顺序问题探讨 在计算机科学中，栈是一种基本但极其重要的数据结构，遵循“后进先出”（LIFO，Last In First Out）原则。在这个问题中，我们关注的是如何通过一系列的push（入栈）和pop（出栈）操作，从给定的操作数序列1, 2, ..., n中生成所有可能的输出序列，特别是当栈A的深度大于操作数序列的长度n时。 首先，理解栈的基础操作至关重要。push操作将元素添加到栈顶，而pop操作则移除栈顶的元素并返回其值。在宁宁同学提出的问题中，他考虑了两种主要操作： 1. **Push操作**：从操作数序列头部移一个元素到栈顶，这相当于在栈中增加一个元素。 2. **Pop操作**：从栈顶移一个元素到输出序列的尾部，即执行栈的出栈操作。 当初始状态是栈A深度大于n，我们面临的是从n个不同元素中构建所有可能的输出序列。由于栈的特性，每次出栈都必须是从栈顶开始，因此输出序列的顺序依赖于栈内部元素的排列顺序，而这种排列又受到push和pop操作的影响。 对于每个n值，我们可以通过动态规划或递归的方法来计算所有可能的输出序列数量。实验代码中提到的C函数可能是一个递归或迭代的解决方案，它可能采用了回溯策略来枚举所有可能的栈顶元素排列组合。这个函数接受两个参数n（操作数序列长度）和m（栈的初始深度），并返回可能的输出序列总数。 在输入格式中，只有一个整数n，表示操作数序列长度，范围在1到18之间。输出格式则是可能的输出序列总数。样例输入和输出展示了问题的具体应用，比如对于n=3，可能的输出序列总数。 为了得出具体的答案，你需要查看实验代码中的C函数实现，理解其递归或迭代过程。该函数可能会维护一个辅助数据结构，如哈希表或者递归堆栈，用来记录当前状态和可能的后续操作，然后根据这些信息来计算总的输出序列数量。 总结来说，这个问题的核心在于如何利用栈的性质和操作规则来探索所有可能的出栈顺序，通过递归、动态规划或其他算法技巧来解决。实验代码提供了关键的实现框架，阅读并理解这段代码可以帮助你深入理解这个问题及其解决方法。