离散数学：格与布尔代数概念解析

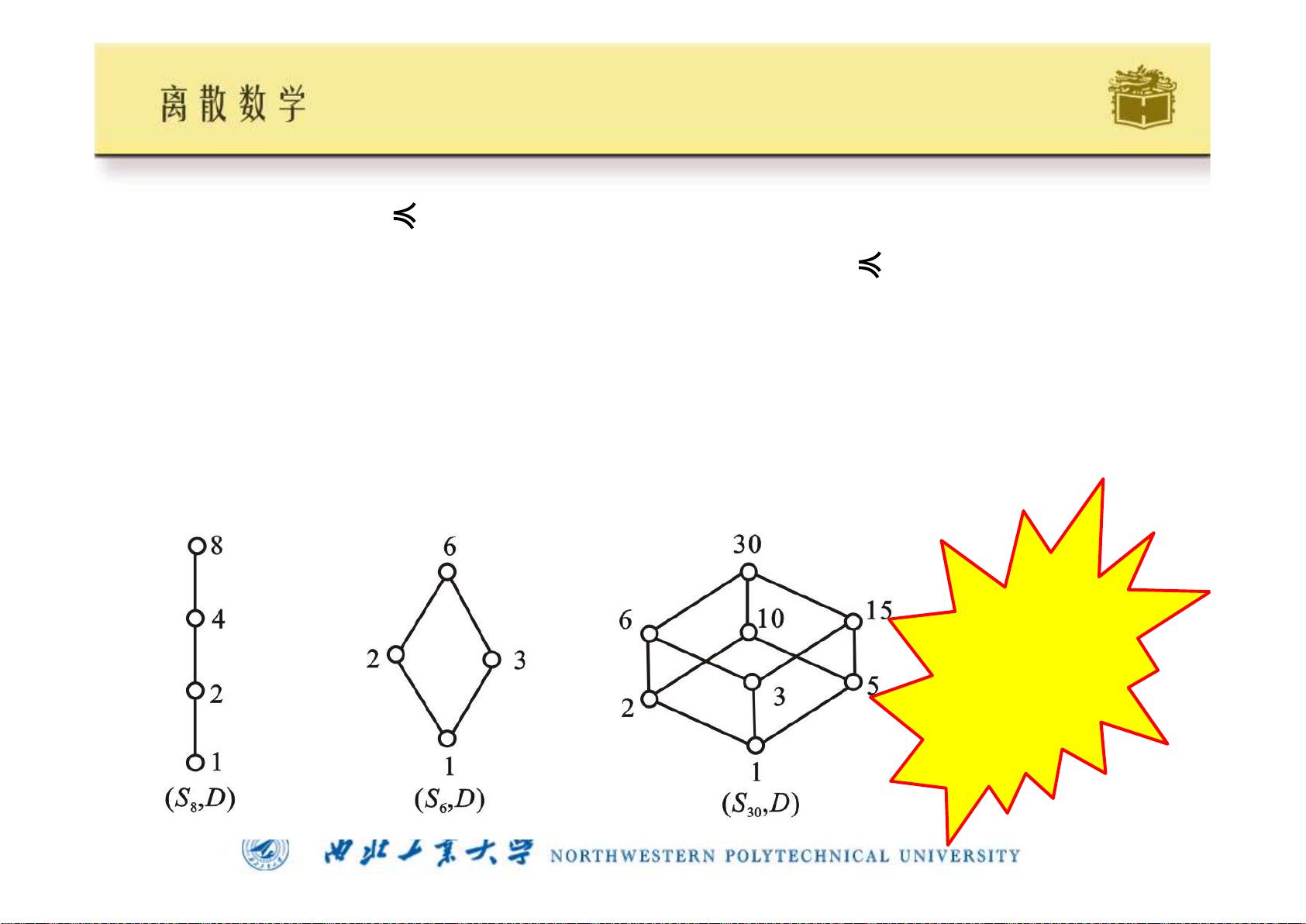
"离散数学中的格与布尔代数概念详解" 本文主要介绍了离散数学中的重要概念——格与布尔代数。格是一类具有特定运算性质的代数结构，而布尔代数则是格的一个特例，广泛应用于计算机科学，特别是在逻辑运算和计算机硬件设计中。 首先，格是由非空集合L以及在其上定义的两个二元运算+和*组成的代数系统，这两个运算必须满足交换律、结合律和吸收律。交换律保证了运算的顺序不重要，结合律确保运算的分组不影响结果，吸收律则意味着某一运算可以“吸收”另一个运算的结果。例如，集合的幂集P(A)和交集、并集运算构成的格，以及正整数的最大公因数和最小公倍数运算构成的格，都是格的实例。 格的性质包括幂等律（任何元素加上自身或乘以自身结果不变），子代数仍然是格（保持运算性质），以及对偶律（公式及其对偶式都是定理）。对偶律是通过将公式中的运算符替换为其对偶来实现的，保持了公理的正确性。 进一步讨论了偏序格的概念，它是偏序集的一种扩展，要求其所有子集都有上确界和下确界。例如，正因子集合关于整除关系构成的偏序集就是偏序格，其中上确界是两数最小公倍数，下确界是最大公约数。 最后，文章给出了两个例子来判断是否构成格。第一个例子是集合B的幂集P(B)关于包含关系构成的偏序集，由于幂集的任何子集都有最大元素（全集）和最小元素（空集），所以它是格。第二个例子是整数集Z关于小于等于关系构成的偏序集，整数集的上确界和下确界不一定存在，因此不是格。 布尔代数是格的一个特殊情况，它除了满足格的性质外，还要求存在恒等元0（吸收元）和1（单位元），并且任何元素都有补元，使得a + a' = 1，a * a' = 0。布尔代数在计算机科学中有着广泛应用，如布尔逻辑、电路设计和数据结构。 总结来说，离散数学中的格与布尔代数提供了理解和分析运算系统的基础理论，它们在算法设计、形式逻辑和计算理论等领域都有着重要的作用。理解这些概念有助于深入学习和应用离散数学知识。