图论算法详解：最大流最小切在图像处理中的应用

"本文主要介绍了图论中的最大流最小切算法，特别针对图像处理的初学者，帮助他们更好地理解和应用图切的知识。" 在图论中，最大流问题是一个非常重要的概念，它常用于解决资源分配、网络传输等问题。长沙市雅礼中学的朱全民所讲述的这个主题，主要是围绕如何在运输网络中最大化从源点S到汇点T的物资运输量。这个问题可以通过构建网络流模型来解决。 网络流图是一个特殊的有向图，其中包含源点S（无入边）和汇点T（无出边），每条边（弧）都有一个非负的容量限制，表示这条边的最大传输能力。一个网络流图G=(V,E,C)满足上述条件，其中V是顶点集合，E是边集合，C是边的容量集合。 可行流是指在网络流图中，每条边的流量不超过其容量限制，并且在除了源点和汇点外的所有顶点，其流入的流量等于流出的流量，保证了流量的守恒。可以用一组非负数fij表示每条边的流量，满足以下三个条件： 1. 每条边的流量不超过其容量：fij ≤ Cij。 2. 流量平衡：除源点S和汇点T外，每个顶点vi的总流入流量等于总流出流量。 3. 源点S的总流出流量等于汇点T的总流入流量，表示网络的总流量。 可改进路是寻找能够增加总流量的路径。在给定的可行流中，如果存在一条从S到T的路径P，使得路径上存在非饱和弧（流量未达到容量限制）并且反向弧上有非零流量，那么这条路径就是可改进路。通过调整可改进路上的流量，可以在不违反其他条件的情况下增加总的网络流量。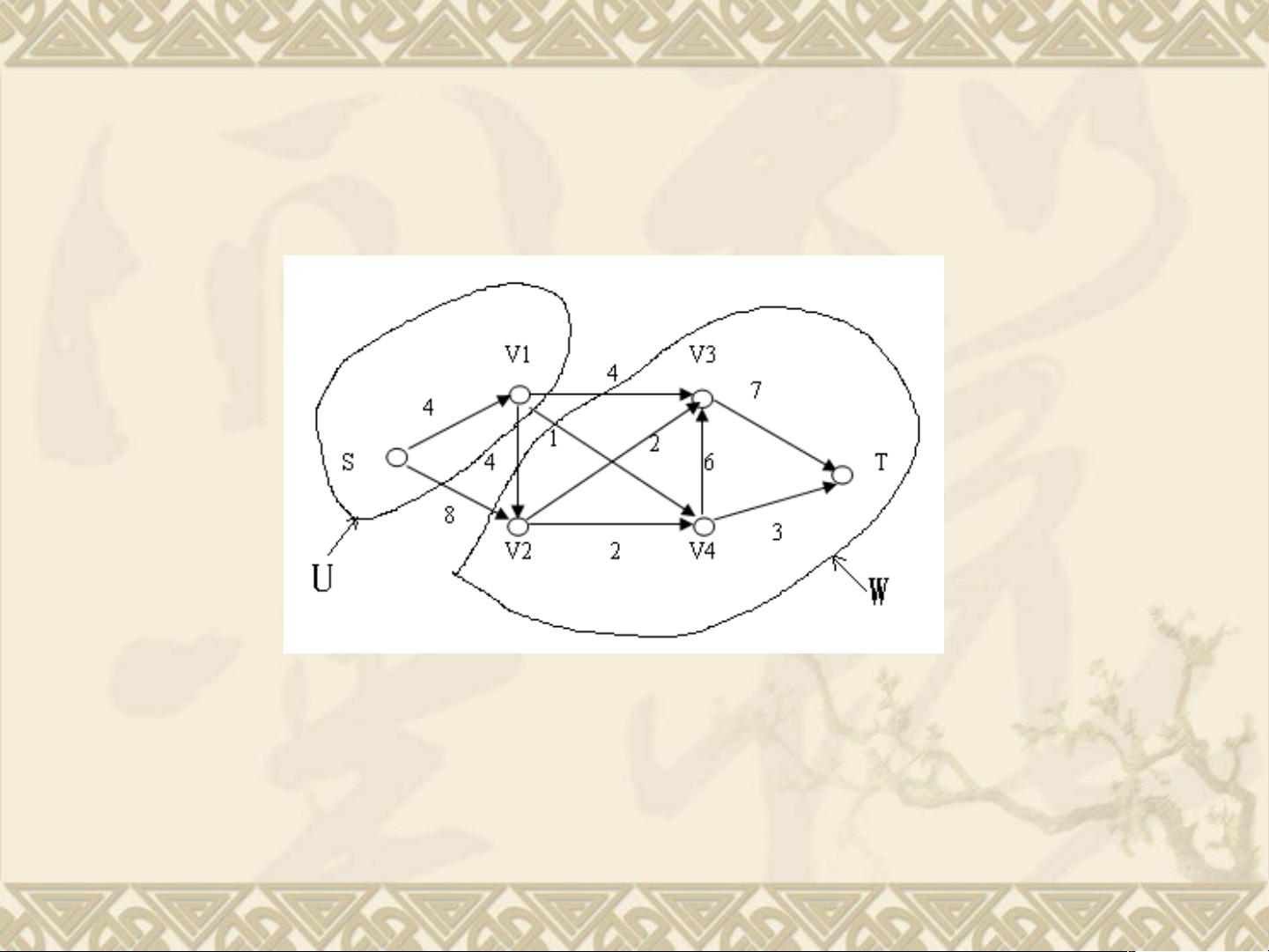 最小割切是最大流问题的另一个关键概念。割切是网络中一部分顶点到另一部分顶点的边的集合，割切将网络分成两个部分，S和T分别位于这两个部分。最小割切是所有割切中容量最小的那个，即允许通过的最小流量。Kolmogorov's Max-Flow Min-Cut Theorem表明，在无容量限制的网络中，最大流的值等于最小割切的容量。 解决最大流问题的方法有很多，例如Ford-Fulkerson方法和Edmonds-Karp算法，它们通过寻找并增加可改进路来逐步提高网络的流量，直到找不到可改进路为止，此时达到的最大流量即为最大流。 在图像处理领域，图论的概念和最大流最小切算法常用于分割、标记、特征检测等问题。例如，可以构建一个图，其中像素是顶点，像素间的相似性或连接关系作为边，通过最大流算法找到最佳的分割方案。 图论的最大流最小切算法是解决资源分配、网络优化等问题的有效工具，其原理和应用广泛存在于各种实际场景中，包括但不限于运输网络设计、电路设计、计算机网络数据传输以及图像处理等。理解并掌握这一算法，对于提升解决问题的能力和效率具有重要意义。