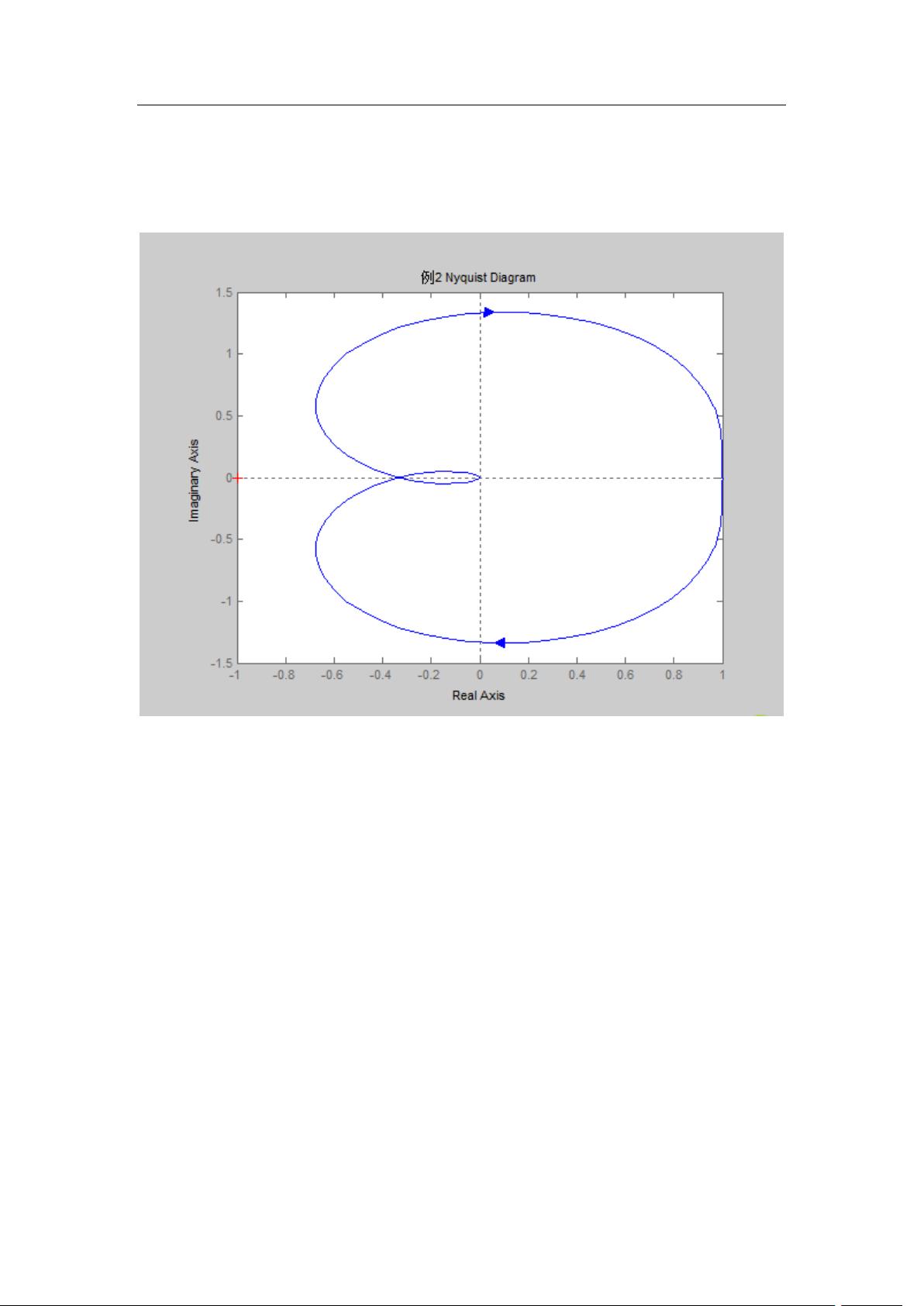
MATLAB控制系统分析：Nyquist图与稳定性判据

"实验七-基于MATLAB控制系统的伯德图及其频域分析 一、实验目的 1、熟悉使用MATLAB绘制控制系统伯德图的过程。 2、掌握通过伯德图分析控制系统频率特性的方法。 3、理解增益裕度和相位裕度的概念及其在系统稳定性中的作用。 4、学习如何通过调整系统参数改善系统的动态性能。 二、实验原理 伯德图是控制系统设计中常用的工具，它展示了系统在不同频率下的增益和相位特性。增益曲线（Bode magnitude plot）表示系统的幅频特性，而相位曲线（Bode phase plot）则展示系统的相频特性。通过伯德图，可以直观地分析系统的稳定性和动态性能。 1、增益裕度：当增益曲线与穿越-180度线的相位线相交时，对应的增益称为增益裕度。如果增益裕度为正，系统在相位裕度耗尽前不会达到振荡条件，系统是稳定的。 2、相位裕度：相位曲线与-180度线的交点表示相位裕度。相位裕度为正值时，系统具有足够的稳定裕度。 三、实验内容 1、绘制控制系统伯德图 例1、系统开环传递函数为，绘制其伯德图。 2 10 () 2 10 Gs s s    M-file clc clearall den=[10]; num=[1210]; sys=tf(den,num); bodeplot(sys); 2、分析系统稳定性与动态性能 例2、已知 绘制伯德图并分析其稳定性与动态响应。 M-file clc clear 3 2 0.5 () () 2 0.5 GsHs s s s    den=[0.5]; num=[1210.5]; sys=tf(den,num); bodeplot(sys); 观察增益曲线和相位曲线，确定增益裕度和相位裕度。 四、实验能力要求 1、熟练使用MATLAB的bodeplot()函数绘制伯德图，理解增益曲线和相位曲线的含义。 2、能够从伯德图中读取增益裕度和相位裕度，评估系统的稳定性。 3、通过调整系统参数，观察伯德图的变化，探究如何优化系统的动态性能和稳定性。 4、结合奈氏图和伯德图，全面理解控制系统在时域和频域的稳定性分析。 五、实验总结 通过实验六和实验七，学生将全面掌握MATLAB在控制系统分析中的应用，包括Nyquist图的绘制和稳定性分析，以及伯德图的制作与性能评估。这为后续的控制系统设计和优化奠定了坚实的基础。" 实验六和实验七的重点在于理解并应用奈奎斯特稳定性判据和伯德图分析控制系统的稳定性。通过MATLAB的nyquist()和bodeplot()函数，学生可以绘制出系统的奈氏图和伯德图，进而分析系统的动态性能和稳定性。实验不仅要求学生熟练操作MATLAB，还强调理论知识与实践的结合，以便于他们在实际工程中解决控制系统的稳定性问题。