A*算法在N码问题中的汉明距离与曼哈顿距离应用

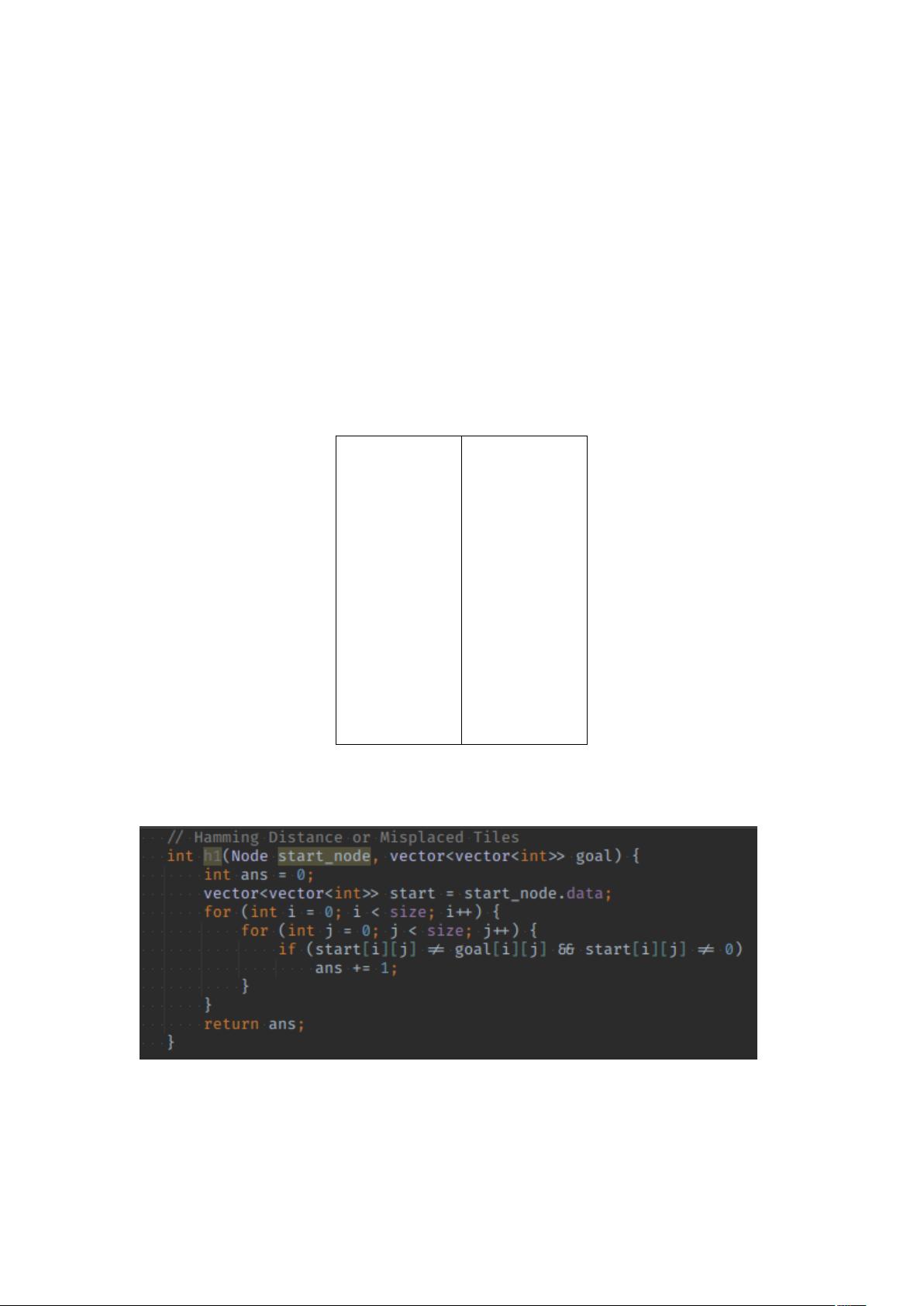
本资源主要讨论了使用A*算法解决N码问题（一种经典的组合优化问题，类似于8-puzzle，目标是将数字按顺序排列）的过程，特别是在寻找最优解的过程中应用的启发式搜索方法。两种关键的启发式函数被探讨：汉明距离和曼哈顿距离。 1. **汉明距离**： 汉明距离是指两个序列中不同元素的个数，不包括'0'。在这个实验中，给定的起始状态1 2 53 0 67 4 8与目标状态1 2 34 5 67 8之间的汉明距离是3，因为错误放置的数字是'5', '3', 和 '4'。虽然汉明距离直观，但它作为启发式搜索的效率较低，因为算法可能需要探索大量节点才能达到目标。 2. **曼哈顿距离**： 曼哈顿距离则是计算每个非'0'数字在起始状态和目标状态中的绝对偏移量之和。对于示例输入，起始状态的曼哈顿距离为8，涉及数字'5', '3', '4', 和 '8'。曼哈顿距离的计算更为高效，因为它减少了不必要的搜索步骤，使得找到解决方案的速度显著提升。 3. **可解性判断**： 对于标准的N码问题，判断是否可解通常通过检查输入状态的逆序对数量。如果数量为奇数，则问题不可解。然而，这里的挑战在于目标状态不是顺序排列的，因此需要对传统方法稍作修改。具体步骤包括将目标状态中的'0'移动到最右侧，记录每个数字的新位置，然后基于这个重新编码的起始状态计算逆序对，以此来确定问题是否可解。 4. **案例分析**： 提供了一个实际案例，起始状态为125 306 748，目标状态为123 456 780。通过A*算法，可以看到耗时、所需步数以及不同启发式方法（汉明距离）的应用结果。汉明距离在此情况下计算得出的时间较长，显示出其搜索效率的局限。 总结，本资源详细介绍了如何利用A*算法解决具有非标准目标状态的N码问题，特别是通过比较汉明距离和曼哈顿距离这两种启发式方法的性能，并结合逆序对理论进行问题的可解性判断。这对于理解和实现此类优化问题的求解策略具有重要价值。