傅里叶变换：历史、原理与分类详解

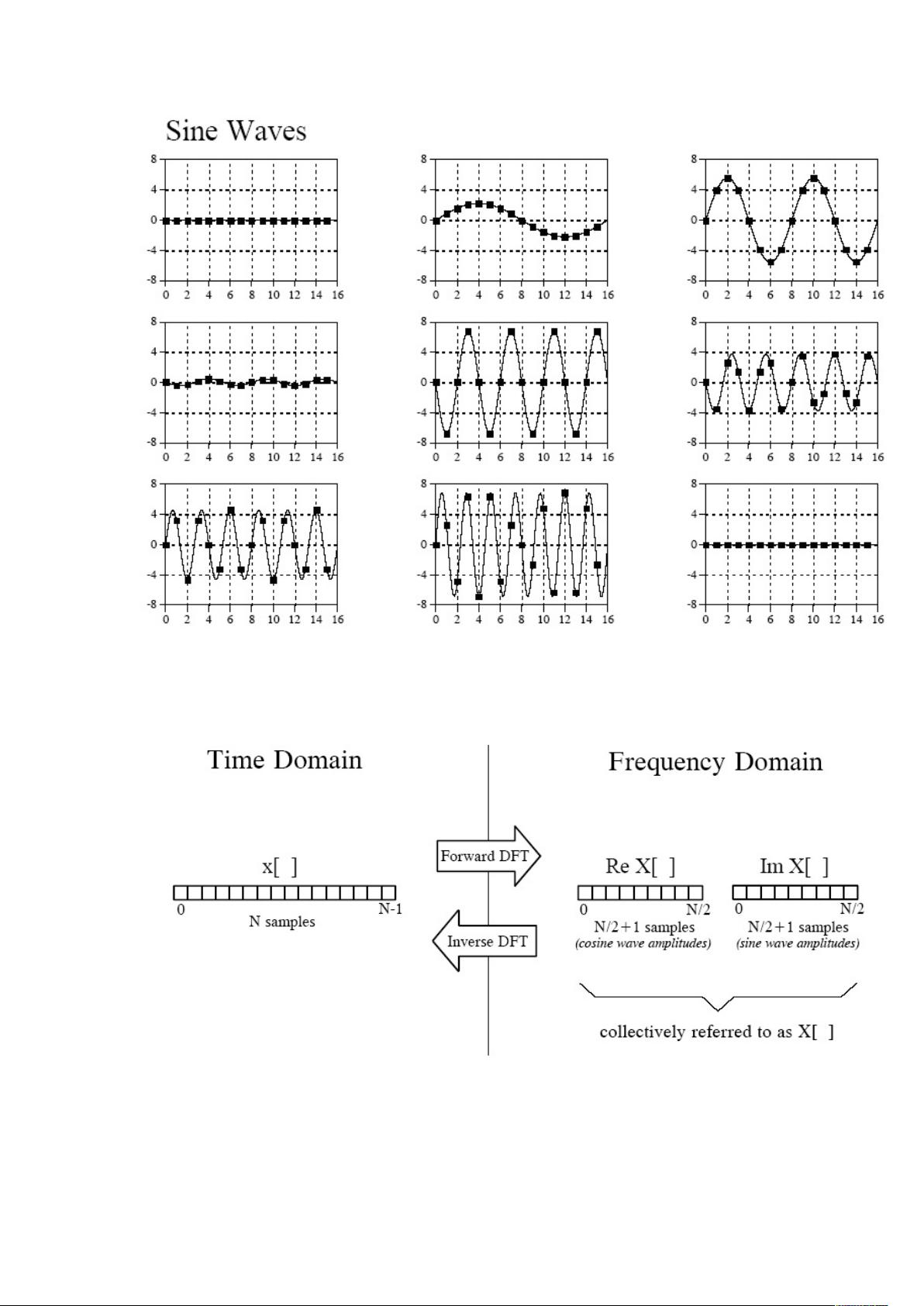
傅里叶变换是数学与物理学中一项重要的工具，它由法国数学家傅里叶提出，最初是为了描述温度分布中的周期性现象。傅里叶变换的核心概念在于，任何连续周期信号都可以由一系列正弦或余弦函数的线性组合来表示，尽管对于非连续信号如方波，正弦曲线无法精确地复制其棱角特性，但可以通过无限逼近的方式实现，这种方法的优势在于正弦函数能够保持信号的频率和波形不变，仅改变幅度和相位，这是其他函数如方波或三角波所不具备的特性。 傅里叶变换的分类主要依据信号的类型： 1. **非周期性连续信号**：这里的傅立叶变换，通常指的是连续时间傅里叶变换（Continuous-Time Fourier Transform），它将非周期信号分解为不同频率成分的组合，便于分析信号的频域特性。 2. **周期性连续信号**：傅立叶级数是针对这类信号的特例，它描述的是一个函数在其周期内的展开，由一系列周期正弦或余弦函数组成，用于解决周期性问题。 3. **非周期性离散信号**：在数字信号处理领域，对于非周期性信号，我们会采用离散时间傅立叶变换（Discrete-Time Fourier Transform，DTFT），它将离散时间序列转化为频域信号，便于分析频域特性，尤其是在通信和信号处理中应用广泛。 4. **周期性离散信号**：离散傅立叶变换（Discrete Fourier Transform，DFT）是针对周期性离散信号的，它是DTFT的特殊情况，计算简便且适用于计算机实现，DFT是数字信号处理中的基础工具，常用于滤波、频谱分析等任务。 理解傅里叶变换的关键在于理解其背后的原理和应用场合，它不仅在理论研究中有重要地位，也在实际工程实践中发挥着核心作用，如音频和视频编码、通信系统的设计、信号滤波等领域。掌握傅里叶变换不仅有助于深入理解信号的本质，还能提升在解决复杂工程问题时的效率和精度。