分布式 Gibbs 抽样：潜在狄利克雷分配的细节解析

"这篇文档是关于Latent Dirichlet Allocation（LDA）的详细解析，主要探讨了如何在生成模型中推断参数。作者在尝试理解LDA的过程中，发现缺乏全面且包含所有必要细节的文档，因此决定撰写这篇文章。文中提到了对分布式Gibbs采样的应用，并对现有的LDA Gibbs采样器代码进行了分析，但指出这些代码并未展示数学推导过程。此外，作者参考了Griffiths的论文和报告，以及一篇由Gregor Heinrich撰写的primer，尽管这些资料提供了一些帮助，但仍存在缺失和不完整性。作者旨在通过此文档弥补这一空白，为读者提供一个关于LDA的全面指南，特别是集中在LDA的数学推导和实现细节上。" Latent Dirichlet Allocation（潜在狄利克雷分配）是一种在自然语言处理和机器学习领域广泛使用的主题模型。它假设文本数据是由多个隐含的主题生成的，每个主题又由一组概率分布的词汇组成。LDA是一种生成模型，因为它可以用来模拟数据的生成过程。在LDA中，我们有以下关键概念： 1. **文档（Documents）**：一系列的词（词频）组成的文章或文本片段。 2. **主题（Topics）**：一组概率分布的词汇，代表文档中的一类共现模式或概念。 3. **词汇表（Vocabulary）**：所有可能出现的单词集合。 4. **词项（Words）**：文档中的单个单词。 5. **狄利克雷分布（Dirichlet Distribution）**：用于模型参数的先验分布，这里是指主题和文档之间的分配比例。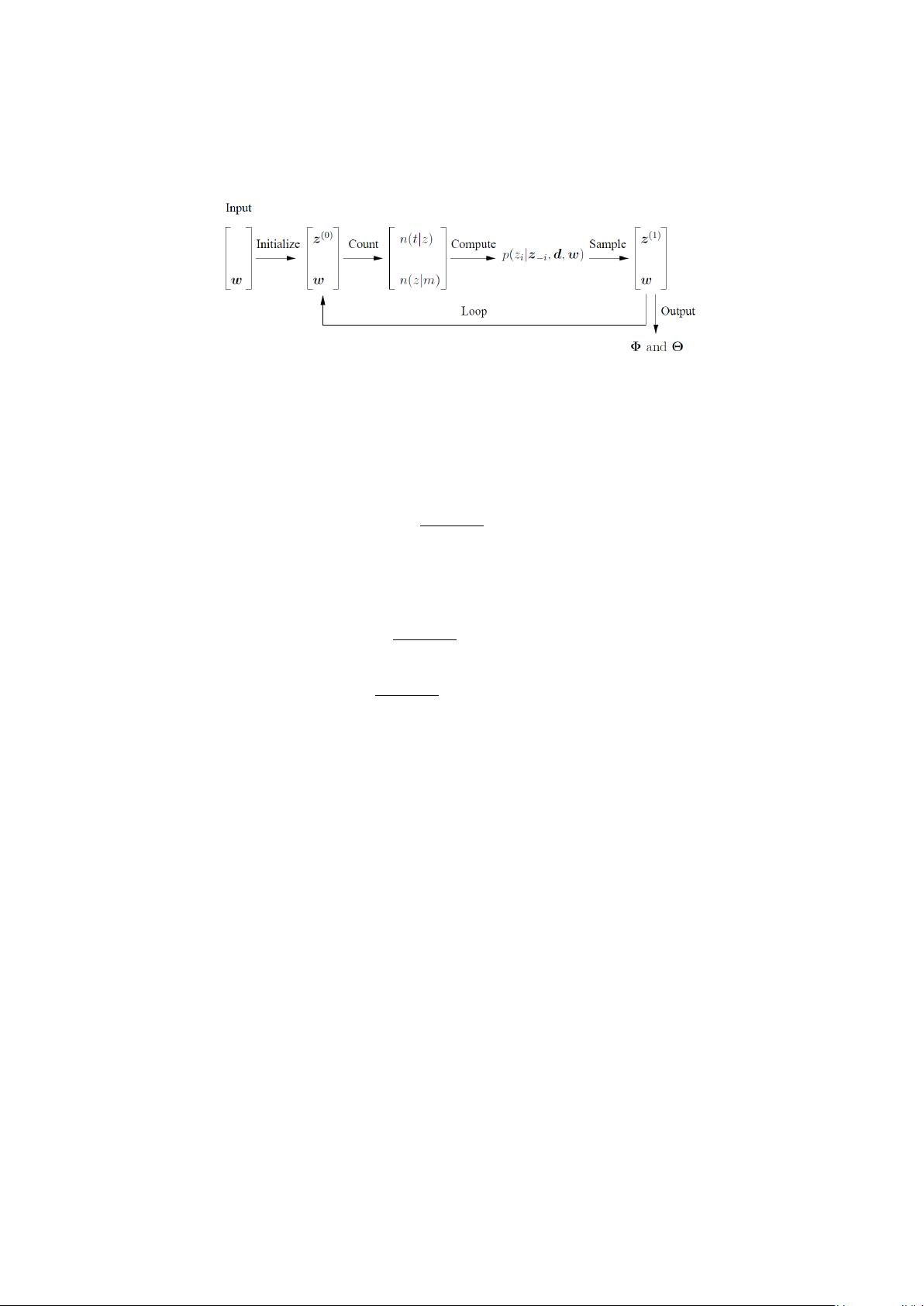 在LDA模型中，每个文档都有一个主题分布，而每个主题都有一个词汇分布。这些分布都是随机的，并且在模型训练过程中通过迭代优化来学习。**Gibbs采样**是LDA中常用的一种近似推理方法，用于从后验概率分布中采样模型参数。通过反复修改文档中每个词所属主题的假设，直到系统达到稳定状态，从而获得文档和主题的最优配置。 在分布式环境中，如Hadoop的MapReduce框架，可以实现大规模数据集上的Gibbs采样，提高LDA的计算效率。然而，代码实现通常只关注算法的实现，而忽略了背后的数学原理。因此，作者在文档中强调了数学推导的重要性，以帮助读者深入理解LDA的工作机制。 在实际应用中，LDA可以用于信息检索、文本分类、推荐系统等领域。通过识别文本的主题结构，我们可以更好地理解文档内容，进行文档聚类，甚至预测用户兴趣。然而，LDA的参数选择（如主题数量）、初始化策略和迭代次数等都对模型性能有很大影响，这也是实践中需要考虑的问题。 LDA是一种强大的工具，用于从大量文本数据中抽取出隐藏的主题结构。通过理解和掌握LDA的数学基础，开发者和研究人员能够更好地利用这个模型解决实际问题。这篇文档的目的就是提供这样一个全面的指南，帮助读者深入理解LDA的细节，并能有效地实现和应用LDA模型。