scikit-learn 0.19：线性模型与岭回归解析

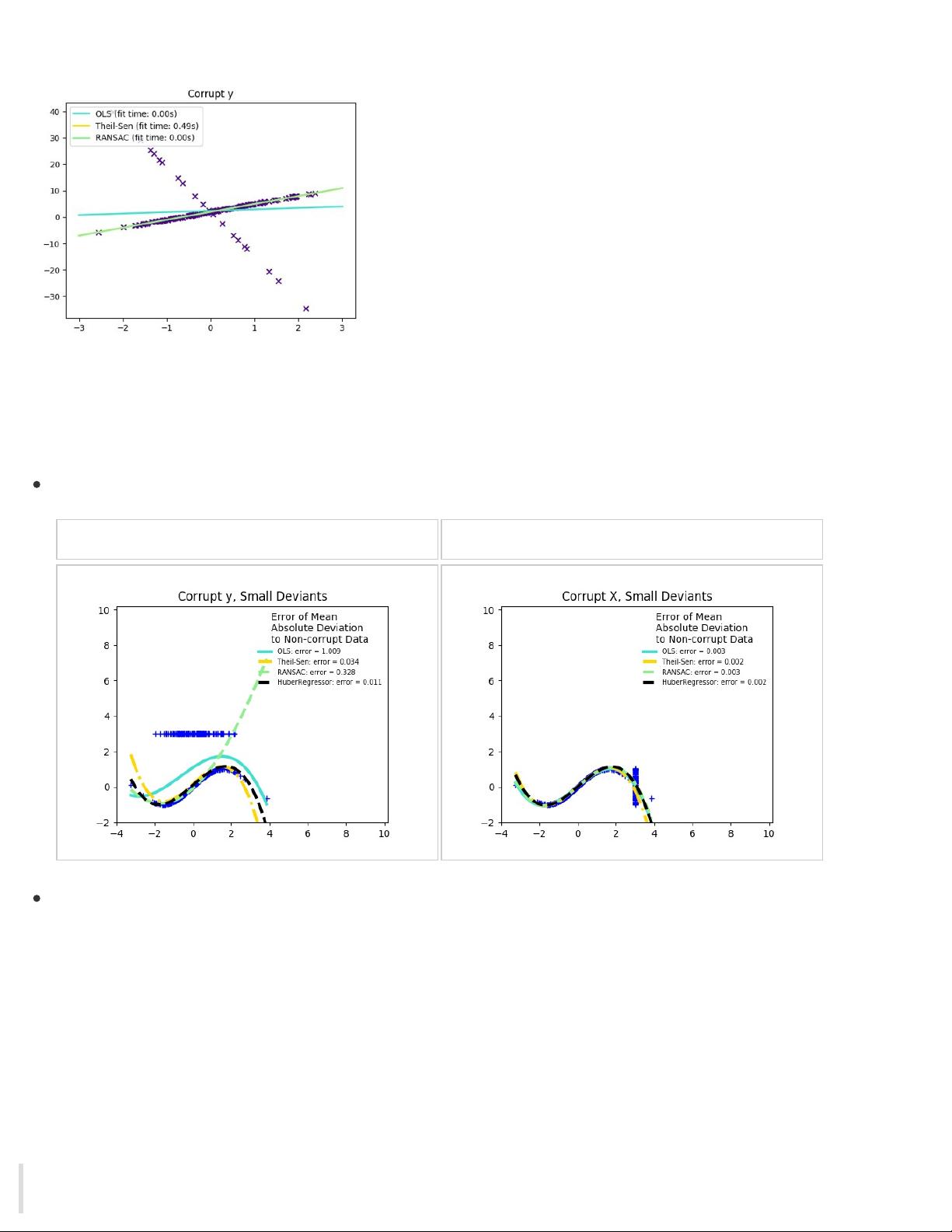
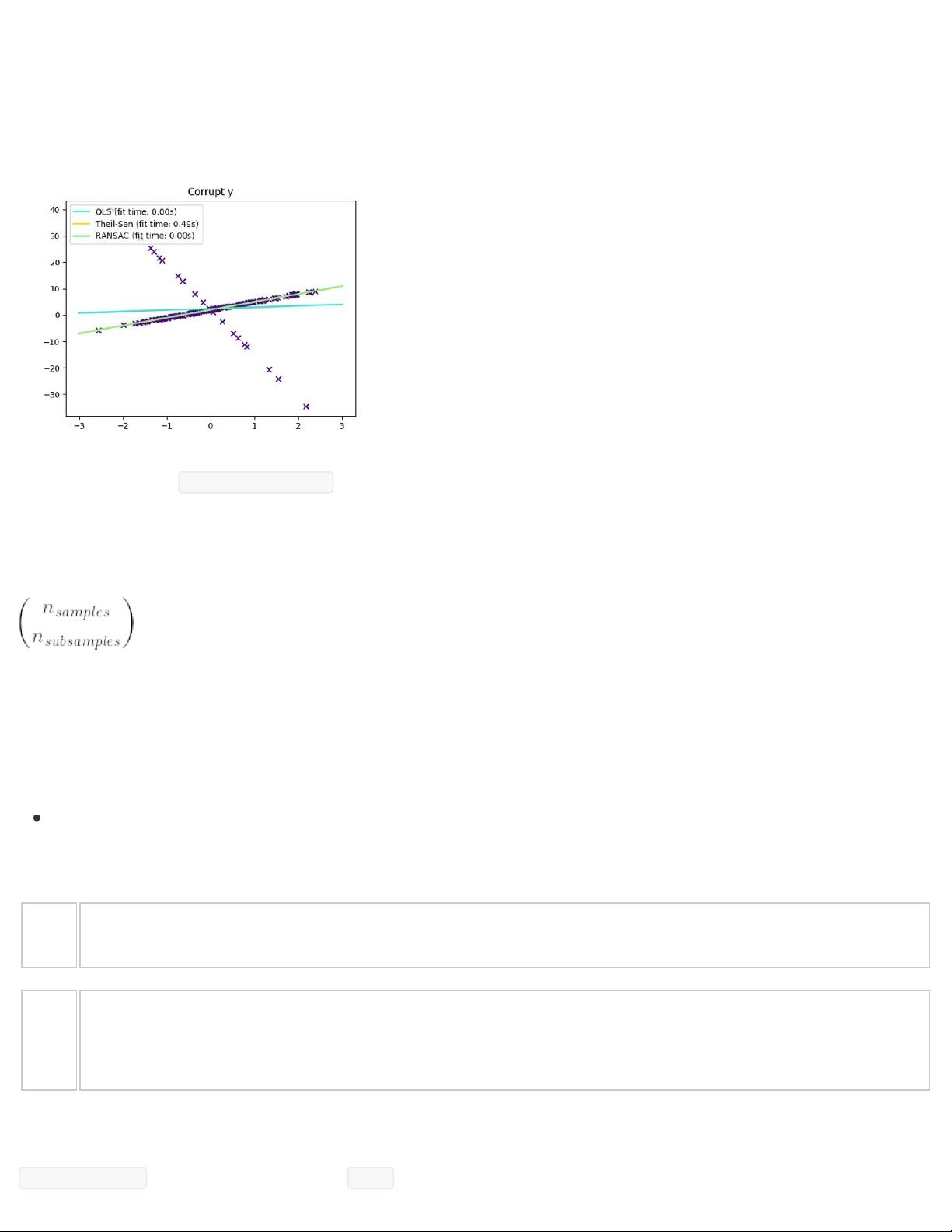
"scikit-learn 0.19 中文文档包含了关于广义线性模型、普通最小二乘法和岭回归等机器学习技术的详细介绍。这些文档为学习scikit-learn库提供了中文版的参考资料，适合初学者和有一定基础的Python开发者使用。" 在scikit-learn 0.19版本的文档中，广义线性模型（Generalized Linear Models, GLMs）是一个重要的部分，它包括一系列回归方法，其中的目标变量y是输入变量x的线性组合。GLMs在数学上定义为预测值value是输入变量的线性函数，通过特定的链接函数与期望值相关联。在模块中，系数由`coef_`表示，截距由`intercept_`表示。 1.1.1. 普通最小二乘法（Ordinary Least Squares, OLS） 普通最小二乘法是一种广泛使用的线性回归方法，它通过最小化观测值与预测值之间的残差平方和来拟合模型。在scikit-learn中，`LinearRegression`类实现了这个方法。当模型被fit后，系数会存储在`coef_`属性中。然而，当输入特征之间存在高度相关性（多重共线性）时，OLS可能会导致不稳定的系数估计，增加预测的方差。 例如： ```python from sklearn import linear_model reg = linear_model.LinearRegression() reg.fit([[0,0],[1,1],[2,2]], [0,1,2]) print(reg.coef_) # 输出: array([0.5, 0.5]) ``` 1.1.1.1. 普通最小二乘法复杂度 该方法通过计算X的奇异值分解（SVD）来求解最小二乘问题。对于大小为(n,p)的矩阵X，计算复杂度大约为O(np^2)。 1.1.2. 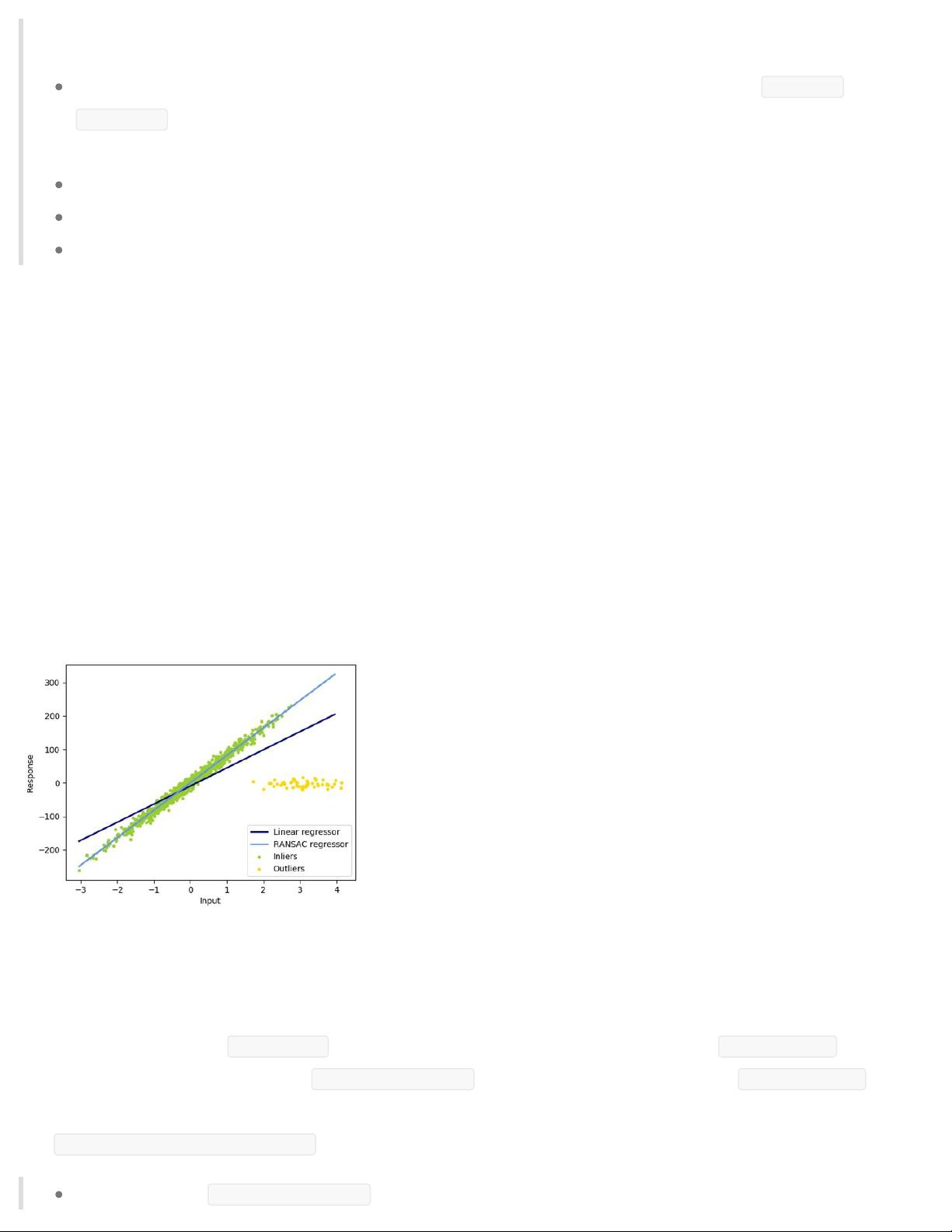岭回归（Ridge Regression） 为了克服普通最小二乘法在面对共线性问题时的不稳定性，岭回归引入了一个正则化项，即L2范数的惩罚。通过调整超参数`alpha`，可以控制系数的收缩程度。当`alpha`增大时，系数会变得更小，从而提高了模型对共线性的鲁棒性。在scikit-learn中，`Ridge`类实现了岭回归，同样使用`fit`方法来拟合模型并存储系数。 ```python from sklearn.linear_model import Ridge ridge_reg = Ridge(alpha=1.0) ridge_reg.fit([[0,0],[1,1],[2,2]], [0,1,2]) print(ridge_reg.coef_) # 输出: 系数在普通最小二乘基础上进行了收缩 ``` 这些模型在机器学习中具有广泛的应用，如数据预测、特征选择以及建模等。通过scikit-learn提供的接口，用户可以方便地实现和评估这些模型，进行各种数据分析任务。文档中的内容详尽易懂，为学习和使用scikit-learn提供了有力的支持。