清华大学计算机科学系详解：小波变换原理与应用

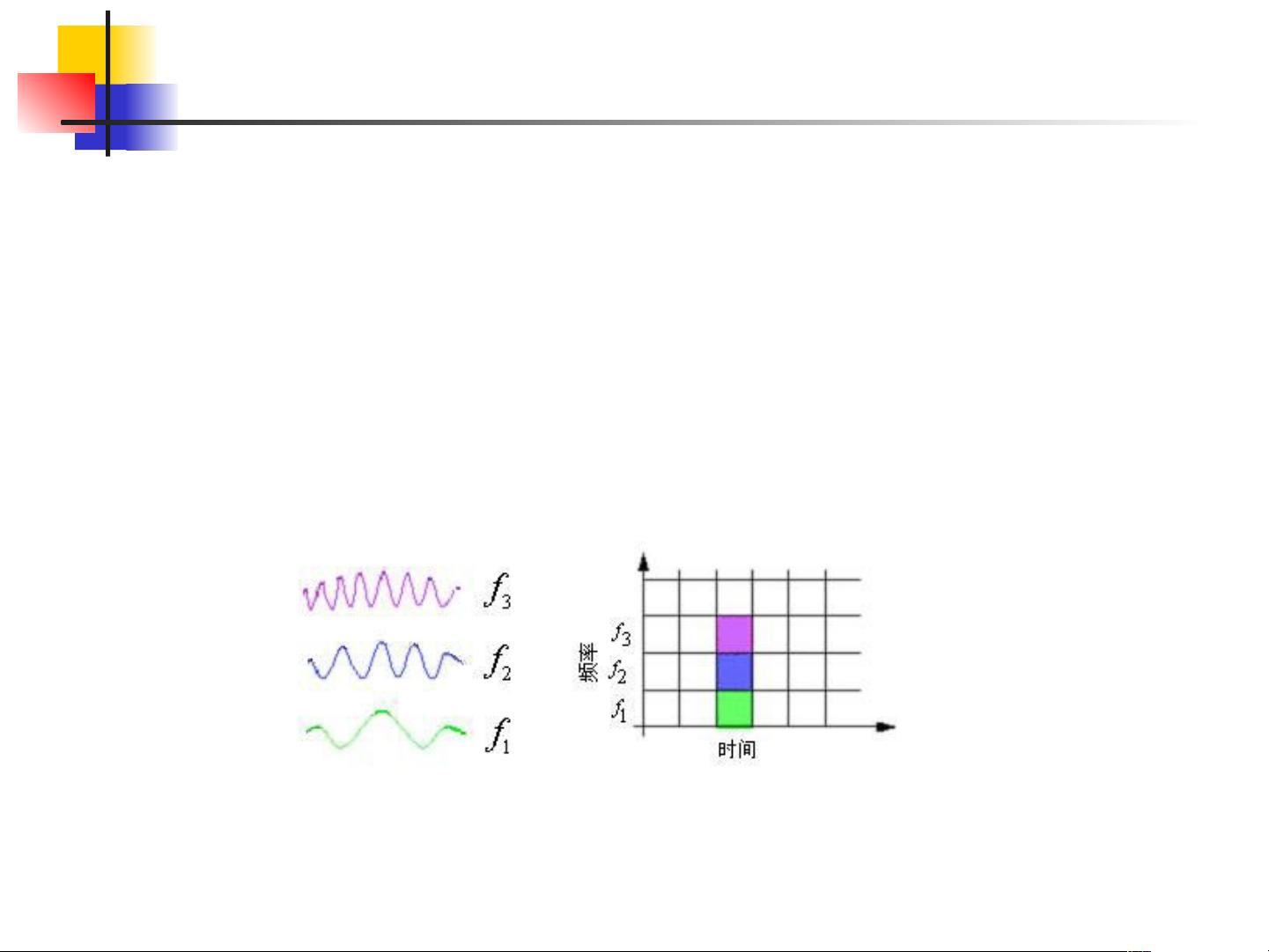
本章节详细介绍了小波变换在计算机科学与技术领域中的应用，特别是通过清华大学计算机科学与技术系林福宗教授的视角来探讨这一主题。小波变换是一个关键的信号处理工具，它结合了傅立叶变换的时间分辨率和局部化的频率分析特性，使得在处理时变信号时更为高效。 首先，7.1节对小波进行了概述，解释了什么是小波，它是一种在有限时间内具有有限持续时间和突发频率变化的数学函数，其平均值必须为零。部分小波如Moret、Grossmann-Morlet的db6函数被广泛用于实际应用中，如图7-1所示的正弦波与小波对比，突出了小波的局部性和多尺度分析能力。 接下来，章节回顾了傅立叶理论，强调了傅立叶变换主要提供频率分辨率，但缺乏时间定位信息。相比之下，小波变换的引入解决了这一问题，它能够同时解析信号的时间和频率特性，这是传统的傅立叶变换所不具备的。 7.2节深入讨论了哈尔函数，这是一种特殊的小波函数，包括哈尔基函数和哈尔小波函数。这部分还涉及到函数的规范化过程，确保分析结果的稳定性和一致性。哈尔基的结构分析有助于理解小波变换的内在机制。 7.3哈尔小波变换是核心内容，这里讲解了如何使用哈尔函数进行信号的分解和重构，以及其在信号处理中的实际应用步骤。通过这个过程，信号可以被分解成不同尺度和频率的成分，便于进一步分析和特征提取。 7.4节专门探讨了规范化算法，这是确保小波变换结果准确性的关键步骤，它涉及到数据预处理和误差控制，确保了变换结果的可靠性和有效性。 最后，7.5部分深入到二维小波变换，介绍了二维小波变换的两种方法，包括一个具体的二维小波变换例子和通用的二维小波变换流程。这对于处理多维图像和信号数据至关重要，因为它能够捕捉到空间和频率维度上的复杂结构。 这一章节不仅涵盖了小波变换的基本概念，还深入到了其实现细节和应用场景，对于理解和应用小波分析技术在多媒体信号处理中的作用非常有帮助。无论是理论基础还是实际操作，都是从事计算机科学和技术领域的学生和专业人士不可或缺的知识。