清华大学计算机科学与技术系小波变换教程

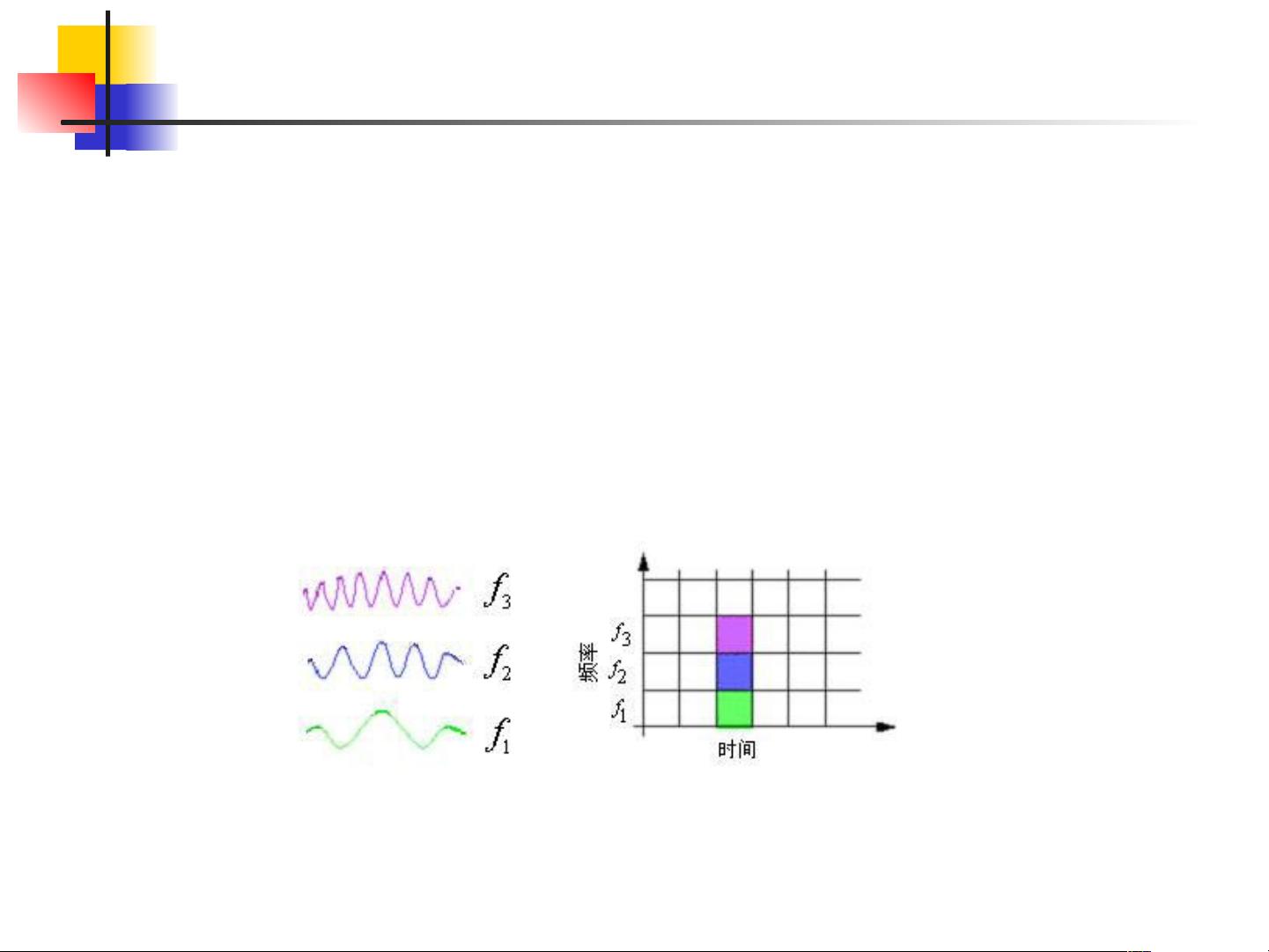
"清华大学小波与小波变换课件，由林福宗教授讲解，涵盖了小波的基础知识、哈尔函数、小波变换及其在多媒体技术中的应用。" 小波与小波变换是信号处理和图像分析领域的重要工具，它结合了时间与频率分析的优点，能对信号进行多尺度分析。本课件出自清华大学计算机科学与技术系，由林福宗教授主讲，主要介绍了小波理论的基本概念和应用。 1. **小波简史**：小波分析的起源可以追溯到1807年Joseph Fourier提出的傅立叶理论，该理论认为任何连续信号都可以表示为一系列正弦和余弦函数的和，即傅立叶展开。随着时间的推移，人们逐渐认识到傅立叶变换在时间定位上的局限性，从而催生了小波变换的发展。 2. **小波概念**：小波是一种在有限时间内具有有限能量的函数，其平均值为零，具备同时刻画信号在时间域和频率域特征的能力。小波的特点在于它们可以精细地捕捉信号的局部特性，尤其是在非平稳信号分析中显得尤为重要。 3. **小波分析**：小波分析是研究信号在不同尺度和位置上的表示，它通过小波函数的平移和缩放操作来实现。这种分析方法提供了良好的时间和频率局部化特性，使得信号的局部特征能够被有效地提取。 4. **小波定义**：小波函数通常是一组经过尺度和位置调整的基函数，它们满足一定的正交性和归一化条件，可以用来分解和重构信号。 5. **哈尔函数**：哈尔函数是小波分析中的一类特殊基函数，包括哈尔基函数和哈尔小波函数。哈尔基函数是一类具有简单结构的离散小波基，而哈尔小波函数则是由哈尔基函数通过缩放和平移得到的。 6. **规范化算法**：在小波分析中，规范化算法是用来确保小波基函数满足正交性或紧支撑性的过程，这对于保证小波变换的稳定性和解析能力至关重要。 7. **二维哈尔小波变换**：在图像处理中，二维小波变换是将分析扩展到二维空间，可以应用于图像的压缩、去噪和特征提取。它包括具体的变换方法，如二维小波变换举例和二维小波变换的计算步骤。 小波变换在多媒体技术教程中占有重要地位，因为它在图像处理、语音识别、信号压缩、故障诊断等多个领域都有广泛应用。通过学习清华大学的这门课件，读者可以深入理解小波理论，并掌握如何利用小波变换进行实际问题的解决。