图布局算法详解：可视化与历史回顾

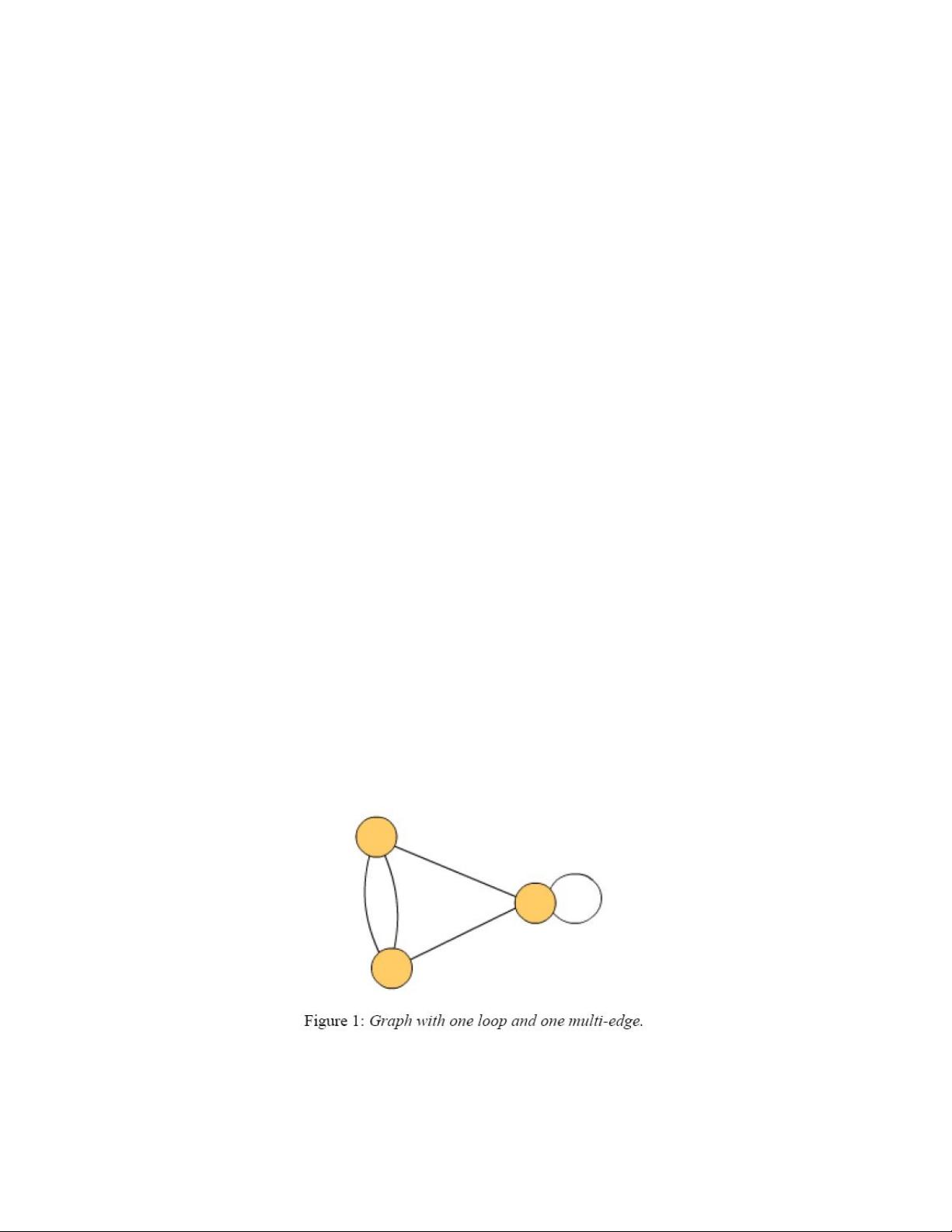
本文是一篇深入探讨图布局算法的综述文章，作者Boštjan Pajntar来自南斯拉夫Jozef Stefan Institute的知识技术部门。文章旨在帮助读者理解和选择最适合可视化工件关系数据的算法，同时提供了一个历史视角，回顾了图布局算法的发展历程。 首先，文章指出在信息时代，数据的规模迅速扩大，传统的信息获取方式转变为挖掘有价值的信息。为了更有效地传达这些大数据，可视化的需求应运而生，图形化表示关系数据成为了重要的信息呈现手段。图论在不同的研究文献中可能有不同的定义，但本文采用了一个通用的框架，包括顶点集V、边集E和边缘映射函数λ。简单图指无环且无多重边的图，而有向图则包含方向性的边。 文章强调了图的大小或规模的概念，这里并未采用单一的术语，而是结合了顶点数量和计算复杂度来衡量。根据图的规模，图被分为小、中、大和超大四类： - 小图（规模n*10，通常不超过150个顶点）：适用于各种算法，因为它们的规模较小，可以轻易处理。 - 中图（规模n*100）：可以由多项式时间复杂度的算法绘制，适合在常规屏幕上展示。 - 大图：由于屏幕限制，无法直接绘制，需要通过其他方法如分块或缩放来处理。 对于大图，作者提到了存在的挑战，即如何在有限的屏幕空间内有效地展现复杂的关系网络。这涉及到一系列的算法优化，如力导向布局（Force-Directed Layout）、层次布局（Hierarchical Layout）和分层聚类（Hierarchical Clustering）等，这些算法利用吸引力和排斥力原则、层级结构或聚类分析来组织节点的位置。 此外，文章还可能讨论了其他经典算法，如Fruchterman-Reingold算法、Spring Embedding算法、Kamada-Kawai算法以及Gephi等工具中的算法实现。这些算法各有特点，如Fruchterman-Reingold算法适用于展示大型网络的全局结构，而Spring Embedding则关注保持相邻节点之间的相似距离。 本文通过详细的算法描述，不仅为读者提供了实用的工具选择指南，也揭示了图布局算法在数据可视化的实际应用和研究中的重要性。对于从事数据分析、图形用户界面设计或者网络科学等领域的人来说，这篇文章是一份宝贵的参考资源。