掌握离散系统关键：拉氏变换原理与典型函数变换详解

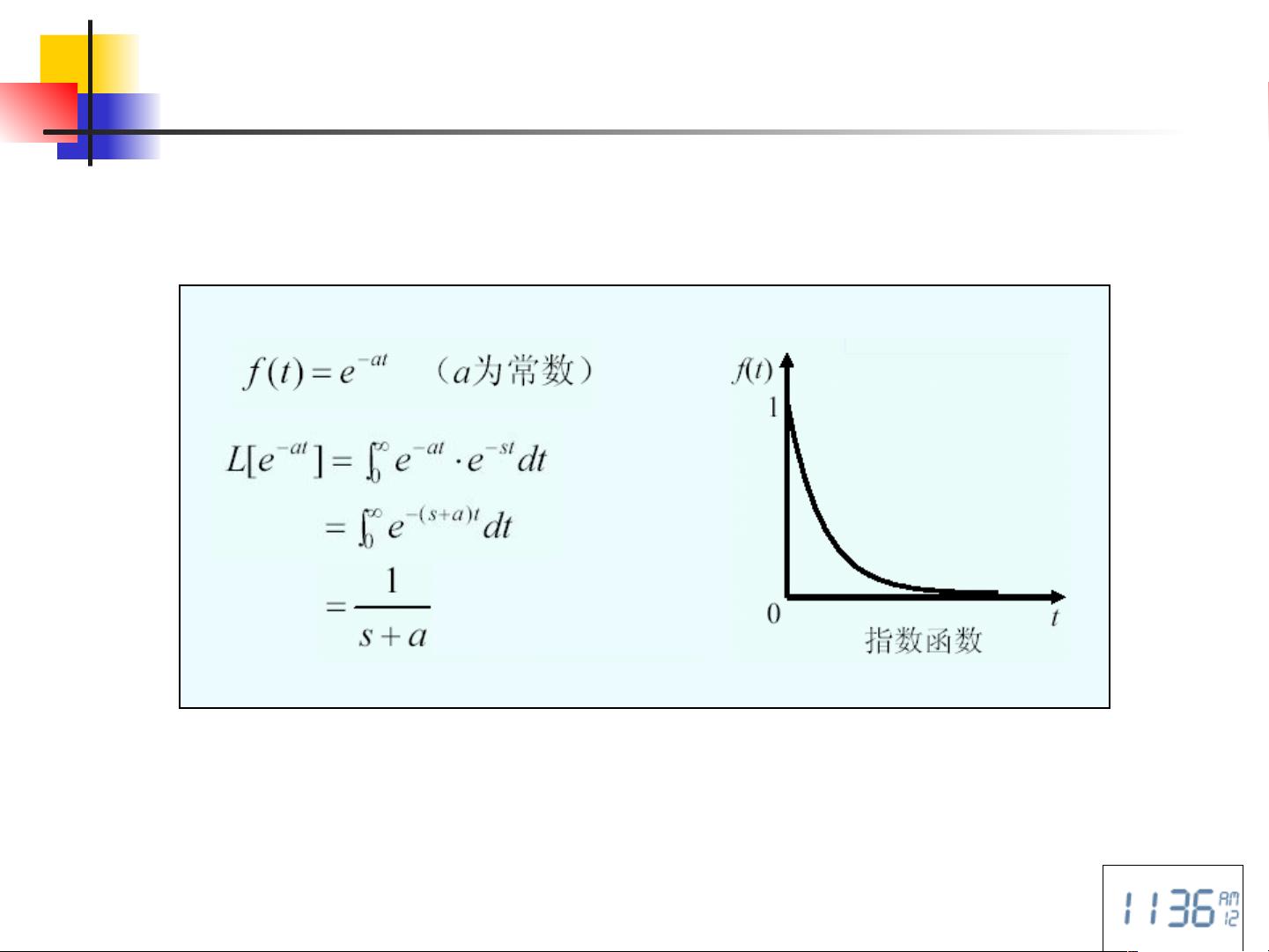
拉氏变换是信号处理和控制系统理论中的一个重要工具，特别是在离散系统分析中占有核心地位。它是一种将时间域中的信号转换到复频域的方法，使得复杂的时域分析可以通过简单的代数运算来完成。拉氏变换的基本定义涉及实函数f(t)，它在t<0时为0，t>=0时其积分在s的某特定区间内收敛。函数f(t)的拉普拉斯变换F(s)由式F(s) = L{f(t)}给出，其中s=σ+jω，σ和ω是实数，L表示拉氏变换操作。 拉氏变换的核心概念包括其定义、反变换以及典型函数的拉氏变换表，如阶跃函数、斜坡函数、单位速度函数、抛物线函数、单位加速度函数、指数函数、三角函数、幂函数等。这些函数的拉氏变换提供了基本的变换规则，对于理解和应用拉氏变换至关重要。 拉氏变换的主要运算定理包括线性定理、微分定理、积分定理、位移定理（包括实位移和复位移）、延时定理、卷积定理、初值定理、终值定理以及比例定理等。这些定理反映了拉氏变换在处理信号处理问题时的性质，如函数的线性组合、导数变换、积分变换、频率响应的计算以及滤波器设计等。 例如，微分定理表明，如果已知函数f(t)的拉氏变换F(s)，那么它的导数的拉氏变换就是F(s)乘以s。而位移定理则指出，如果f(t)的拉氏变换是F(s)，那么f(t-a)的拉氏变换就是F(s)e^{-as}，这对于分析信号的瞬态和稳态行为非常有用。 此外，通过原函数的高阶导数与像函数中s的高次代数式的对应关系，以及原函数乘以指数函数后的变换形式，可以深入理解拉氏变换的内在联系。拉氏变换还与傅里叶变换有相似之处，但更适用于处理非周期性信号。 总结来说，拉氏变换是信号处理中的基础工具，通过掌握其定义、典型函数的变换规则和各种运算定理，工程师们能够有效地分析和设计复杂的控制系统，提升系统性能和效率。学习拉氏变换不仅是对离散系统深入理解的关键，也为后续学习z变换打下坚实的基础。