扩展卡尔曼滤波在机动目标跟踪中的仿真分析

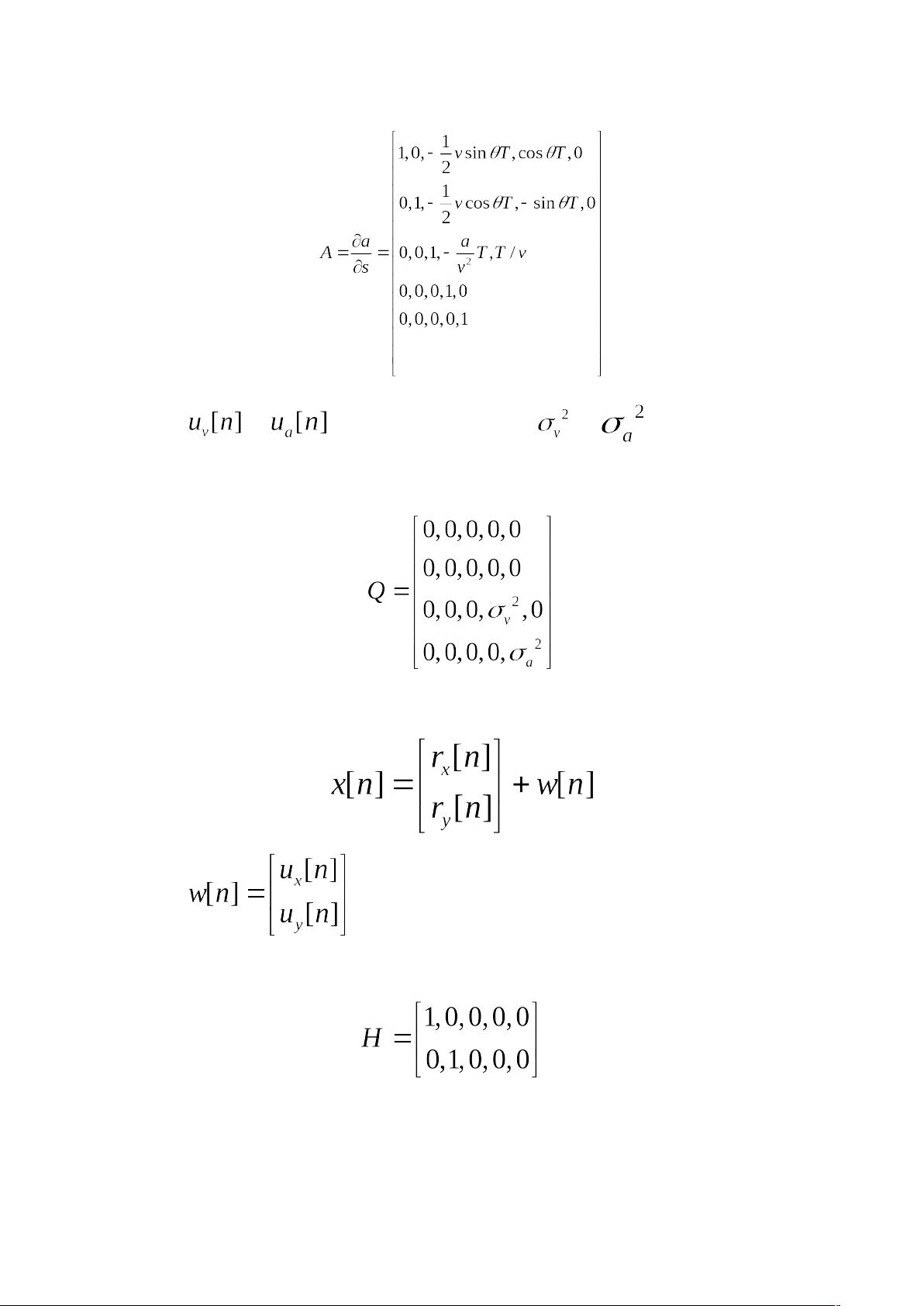
本资源是一份关于统计信号处理的作业，涉及机动目标跟踪的数学建模与卡尔曼滤波算法应用。作业主题围绕机动目标在三个阶段（初始匀速直线、匀速圆周运动和返回匀速直线）下的运动轨迹分析，以及采用扩展卡尔曼滤波进行估计和跟踪。 首先，机动目标在运动过程中，其线速度v保持不变，轨迹切线与横轴正向夹角随时间变化。初始阶段和返回阶段，这个角度分别为0和[pic]。在圆周运动阶段，角速度[pic]从0均匀增加至[pic]。通过这些参数，可以推导出状态变量，如角位置、角速度等，并建立状态方程： 状态方程表示为： 1. [pic]的状态更新公式 2. [pic]的状态转移矩阵，由于角速度和速度的关系，状态转换矩阵为[pic] 3. 驱动噪声的描述，假设噪声不相关，[pic]和[pic]的方差分别为[pic]和[pic] 观测矢量由目标的位置和速度组成，观测矩阵[pic]，噪声分布也考虑了观测值之间的独立性和方差，即[pic]和[pic]的方差分别为[pic]和[pic]。 最后，扩展卡尔曼滤波方程被总结出来，包括预测步骤、更新步骤以及系统噪声模型。滤波器初始化设定为：初始位置[-20000;0]，有偏离可能，速度v=300m/s，角速度[pic]=0，加速度a=0，驱动噪声方差取[pic]=30和[pic]=2。 仿真部分使用MATLAB编程，通过蒙特卡洛方法模拟10次跟踪滤波过程。结果显示，随着滤波器增益M的增大（如M=10和M=1），滤波性能提升，尤其是在目标转弯时表现更好。滤波轨迹、滤波均值轨迹、X和Y方向的滤波估计误差及其标准差都通过图形展示，如图2、图3和图4。附录提供了MATLAB源代码，用于实现整个滤波过程的模拟计算。 这是一份结合理论与实践的统计信号处理作业，展示了机动目标跟踪中的数学建模、卡尔曼滤波算法的实际应用，以及如何通过计算机仿真评估滤波效果。对于学习和研究统计信号处理、雷达目标跟踪或者卡尔曼滤波的学生来说，这份作业具有较高的参考价值。