掌握树状数组:高效查询与修改数据结构
下载需积分: 50 | PPTX格式 | 4.76MB |
更新于2024-07-18
| 8 浏览量 | 举报
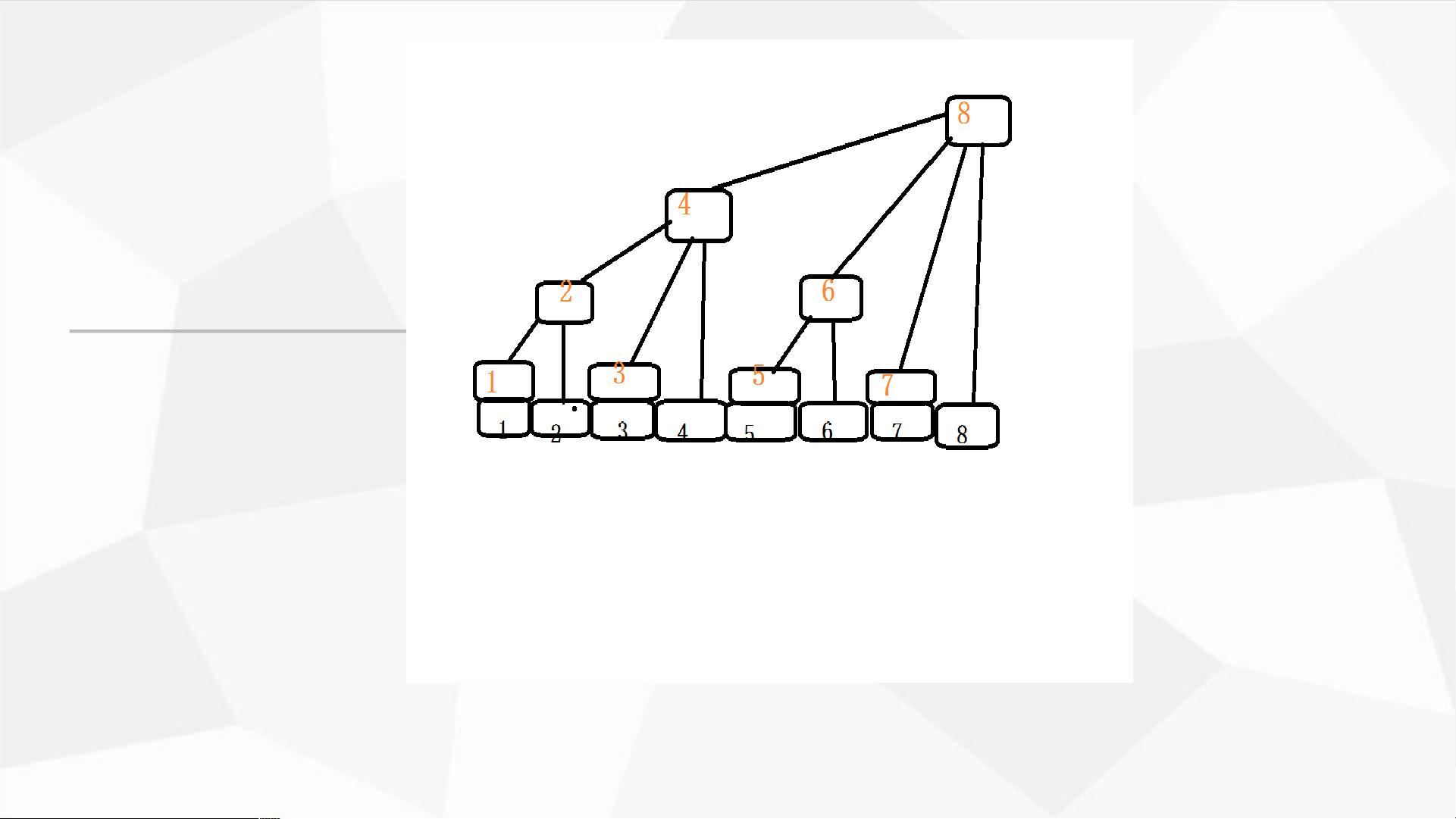
树状数组,也被称为Binary Indexed Tree (BIT) 或 Fenwick Tree,是一种高效的数据结构,其核心在于利用二进制编码来快速实现区间查询和单点修改操作,时间复杂度均为O(log n)。该数据结构特别适用于处理动态范围问题,如求解任意两个索引之间元素的和。
1. **基本概念**:
- **区间查询与修改**:树状数组主要用于高效地执行区间求和,例如计算区间 [L, R] 内所有元素的累计和。然而,每次只能对单个元素进行修改,不能同时更改多个元素的值。
2. **应用场景**:
- **单点修改与区间查询**:在处理一些场景下,如题目中提到的P3374、P3368和P3372,树状数组常被用来解决单点修改后查询整个区间的总和问题,或者反过来,单点查询某个区间内的总和。
- **区间修改**:在一些情况下,如HDU1556 Color the Ball,需要对区间内的元素进行修改,并可能需要查询其他区间的信息,这种功能在树状数组中也能实现。
3. **工作原理**:
- **低位操作**(Lowbit):树状数组通过低位操作来更新元素,即在二进制表示中,将当前元素加上它的最低有效位的值。例如,对于数字3,lowbit(3) = 1,所以更新操作可以表示为 `a[i] += lowbit(a[i])`。
- **递推性质**:计算元素值时,可以根据元素位置的二进制表示来递归地累加前缀和。例如,`a[i] = a[i-1] + c1[i]`,这意味着要计算第i个元素的和,只需累加之前所有元素的贡献。
4. **扩展类型**:
- **前缀和树状数组**:特别用于处理区间单点问题,即直接获取以某个索引为起点的连续子数组的和,无需额外计算。
5. **实现与代码**:
- 代码实现相对简单,主要涉及初始化数组、二进制编码的更新和查询操作,以及理解如何根据lowbit操作进行递归式更新。
树状数组是一种强大的数据结构,它在解决各种区间问题时表现出色,尤其是在需要频繁进行区间查询和单点修改的场景中。理解和掌握其原理和操作方式,对于提高算法竞赛中的效率至关重要。
相关推荐





Simon_Bariona
- 粉丝: 317

最新资源
- MetaTrader 5脚本:iAlligator_HTF绘制鳄鱼指标
- USB micro SMT封装库:全面的原理图与PCB元件资源
- 《古庙全套测绘图纸》- CAD图纸参考下载
- 三星1865型号刷机工具包介绍与使用教程
- 快速搭建Browserify vueify环境,助力Vue 2.0原型设计
- 美国钻石DMM-16-AT操作与技术指南解析
- 市场分析数据对比图表商务PPT模板
- Swift开发的发票计算器应用介绍
- STM32-F0/F1/F2单片机遥控避障巡线小车设计
- Spring5框架学习笔记深度解析
- 手机游戏门户网站模板:单机游戏下载与攻略评测
- JavaSE基础开发:五子棋人机对战小游戏教程
- 易语言实现进程枚举的三种方法详解
- JokerChrome: 探索Chrome生成技术与版本信息
- HTML5打造交互式MP3音乐唱机动画效果
- 商务范工作总结与计划PPT模板设计