图算法探秘：广度优先搜索（BFS）与最短路径

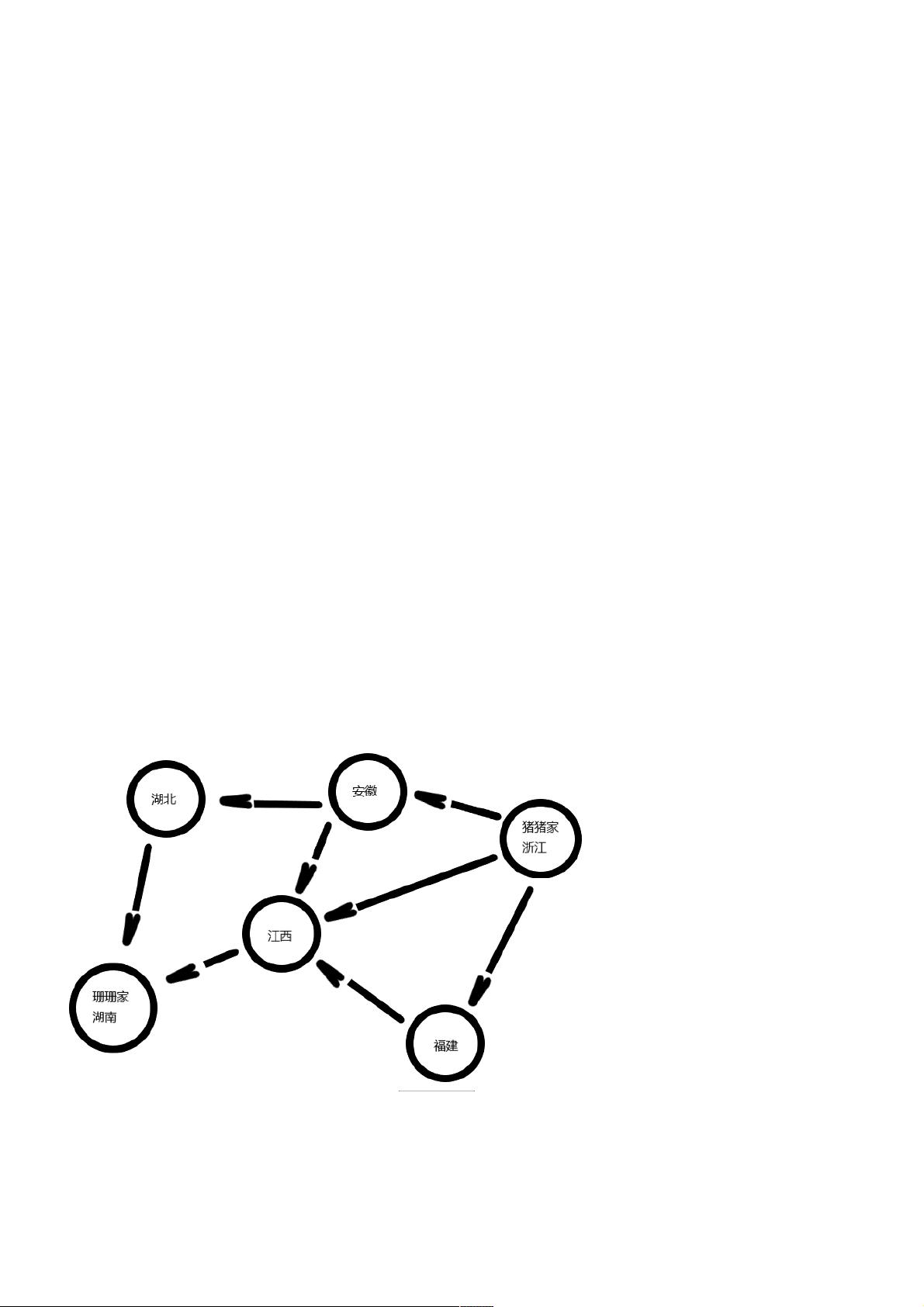
"第六章 广度优先搜索（BFS）" 在计算机科学中，图是一种重要的数据结构，用于表示对象之间的关系。本章主要介绍了如何使用图来构建网络模型，特别是聚焦于广度优先搜索（BFS）算法，这是一种在图中寻找最短路径或验证是否存在路径的有效方法。此外，章节还涵盖了有向图和无向图的概念，以及拓扑排序，这是理解图中节点依赖关系的关键。 1. 图简介 - 最短路径问题：在寻找两个节点间最短路径时，图提供了一种自然的模型。例如，从浙江到湖南的最快路线，希望经过最少的省份。 - 图的定义：图由节点（也称为顶点）和连接节点的边构成。节点可以与多个其他节点相邻，而相邻节点被称为邻居。图可以表示各种实体之间的联系，如城市之间的道路、人际关系等。 2. 广度优先搜索（BFS） - BFS 是一种遍历或搜索树或图的算法，用于寻找从源节点到目标节点的最短路径。它首先访问离起点最近的节点，然后逐步扩展到更远的节点。 - 应用场景：BFS 可用于编写游戏AI，如国际跳棋中计算获胜步数；拼写检查器，计算最小编辑距离以纠正单词；社交网络中查找朋友关系等。 3. BFS 解决的问题 - 存在路径问题：BFS 可以判断两个节点之间是否存在路径。如果在 BFS 过程中到达目标节点，那么存在路径。 - 最短路径问题：对于无权图，BFS 可找到最短路径，因为它是按距离从近到远探索的。在有向图中，BFS 可用于找到最短的层次路径，但不适用于考虑边权重的情况。 4. 队列数据结构 - 在 BFS 中，队列起到关键作用。它按照“先进先出”（FIFO）的原则存储待访问的节点。新发现的邻居被添加到队尾，而当前处理的节点则从队首移除。这确保了节点按照距离的递增顺序进行访问。 5. 实现图和算法 - 使用队列实现 BFS：在Python中，可以使用`collections.deque`来创建双端队列，便于执行入队（enqueue）和出队（dequeue）操作。 - 解决问题：BFS 分两步解决上述问题，首先建立问题的图模型，然后应用 BFS 算法找到最短路径或验证路径的存在性。 6. 运行时间 - BFS 的时间复杂度通常是O(V+E)，其中V是节点的数量，E是边的数量。这是因为每个节点和每条边都会被访问一次。 7. 小结 - 图算法，尤其是 BFS，因其在解决现实世界问题中的广泛应用，如路径规划、关系网络分析等，被认为是非常有用的技术。 通过学习这一章，读者将掌握如何使用 BFS 来解决实际问题，并理解其背后的理论基础，包括图的结构、队列的使用，以及如何在不同场景中应用 BFS 算法。