广度优先搜索(BFS)：Java树结构的高效应用

# 1. 广度优先搜索(BFS)算法概述

广度优先搜索（BFS）算法是一种用于图或树的遍历的算法。其基本思想是从一个节点开始，访问其所有邻近节点，然后对每一个邻近节点再做同样的操作，直到所有的节点都被访问过。这种搜索方式类似于水面上的涟漪扩散，因此得名“广度优先”。

## BFS算法的特点

BFS算法可以保证首次找到目标节点时的路径最短。这是因为BFS每次扩展的是距离当前节点最近的一层，这样就避免了深入一条路径而忽略了可能的更短路径。BFS适合解决如下类型的问题：

- **最短路径问题**：寻找图中两点之间的最短路径。
- **层次遍历**：按层次遍历树或图的所有节点。
- **连通性检测**：判断两个节点是否连通。
## 应用BFS的场景

在现实生活中，BFS算法的应用也十分广泛。例如，在社交网络中寻找某个人与另一个人的最短关系链，或者在网络爬虫中按层级爬取网页。在游戏开发中，它常被用于AI寻路算法，以找到从起点到终点的最短路径。

BFS算法的核心在于使用队列来存储待访问的节点，利用其先进先出（FIFO）的特性，可以保证按照距离源点的远近依次访问节点。这一章，我们将初步了解BFS的工作原理，并为后续章节中树结构的应用打下基础。

# 2. Java树结构基础

### 2.1 树结构的理论基础

#### 2.1.1 树的定义和属性

树是一种非线性的数据结构，它以分层的方式组织数据，模仿了自然界中的树结构。在树结构中，每个元素称为一个节点（Node），节点之间存在父子关系。树由一个根节点（Root）开始，根节点下面可以连接多个子节点，每个子节点又可以有它们自己的子节点，形成一个分层的结构。树结构中，没有父节点的节点称为叶子节点（Leaf Node）。在树的定义中，每一个节点都只有一个父节点（除了根节点），但可以有零个、一个或多个子节点。

树的几个重要属性包括：
- 节点的深度（Depth）：从根节点到当前节点的边的数量。
- 节点的高度（Height）：从当前节点到最远叶子节点的最长边的数量。
- 树的高度：根节点的高度。

### 2.1.2 常见树结构的特点和应用

不同类型的树适用于解决不同类型的问题。以下是一些常见的树结构及其特点和应用：

#### 二叉树（Binary Tree）
二叉树的每个节点最多有两个子节点。二叉树在计算机科学中非常常见，因为它们的算法设计和实现相对简单。常见的二叉树有：
- 完全二叉树（Complete Binary Tree）：除了最后一层外，每层都被完全填满，且所有节点都尽可能地向左。
- 平衡二叉树（Balanced Binary Tree）：任何两个叶子节点之间的高度差都不超过1，常用于实现二叉搜索树，如AVL树、红黑树。

#### 二叉搜索树（Binary Search Tree）
在二叉搜索树中，节点的左子树只包含小于当前节点的数，右子树只包含大于当前节点的数。这种树结构可以高效地支持数据的快速查找、添加和删除。

#### B树和B+树
B树和B+树是多路平衡查找树，被广泛用于数据库和文件系统中，以优化对磁盘的读写。它们的特点是所有叶子节点都在同一层，且所有节点都有子节点。

#### Trie树（前缀树）
Trie树是一种用于快速检索字符串数据集中的键的树形数据结构。它有非常高效的空间利用率，常用于字典的实现和自动补全功能。

#### 红黑树（Red-Black Tree）
红黑树是一种自平衡的二叉搜索树，它在每个节点上增加了一个存储位来表示节点的颜色，可以是红色或黑色。通过对任何一条从根到叶子的路径上各个节点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出两倍，因而是近似平衡的。

### 2.2 Java中树的实现

#### 2.2.1 二叉树的实现

在Java中实现二叉树的基本节点可以这样定义：

class TreeNode<T> {
    T data; // 数据域
    TreeNode<T> left; // 左子节点
    TreeNode<T> right; // 右子节点

    // 构造方法
    public TreeNode(T data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

接下来，我们来构建一个简单的二叉树并进行遍历操作。树的遍历是树操作中非常基础且重要的操作，常见的遍历方式有前序遍历（Pre-order）、中序遍历（In-order）和后序遍历（Post-order）。

以下是使用递归实现的中序遍历算法：

public void inorderTraversal(TreeNode<Integer> root) {
    if (root == null) {
        return;
    }
    inorderTraversal(root.left);
    System.out.print(root.data + " "); // 访问节点
    inorderTraversal(root.right);
}

#### 2.2.2 N叉树的实现

对于N叉树，我们可以采用类似的方法，只是在节点定义中将子节点定义为列表：

class NTreeNode<T> {
    T data;
    List<NNode<T>> children;

    public NTreeNode(T data) {
        this.data = data;
        this.children = new ArrayList<>();
    }
    // 添加子节点
    public void addChild(NNode<T> child) {
        children.add(child);
    }
}

N叉树的遍历相对复杂，我们通常需要使用循环或递归来实现。这里提供一个递归实现的前序遍历：

public void preorderTraversal(NNode<Integer> root) {
    if (root == null) {
        return;
    }
    System.out.print(root.data + " "); // 访问节点
    for (NNode<Integer> child : root.children) {
        preorderTraversal(child); // 递归遍历子树
    }
}

#### 2.2.3 树的遍历算法

我们可以通过递归或迭代的方式来实现树的遍历。遍历算法可以分为深度优先搜索（DFS）和广度优先搜索（BFS）。深度优先搜索通常通过递归实现，而广度优先搜索则通常通过使用队列实现。

这里，我们将展示使用队列实现的二叉树的层序遍历（BFS）：

public void levelOrderTraversal(TreeNode<Integer> root) {
    if (root == null) {
        return;
    }
    Queue<TreeNode<Integer>> queue = new LinkedList<>();
    queue.offer(root);

    while (!queue.isEmpty()) {
        TreeNode<Integer> currentNode = queue.poll();
        System.out.print(currentNode.data + " "); // 访问当前节点
        if (currentNode.left != null) {
            queue.offer(currentNode.left);
        }
        if (currentNode.right != null) {
            queue.offer(currentNode.right);
        }
    }
}

### 2.3 树结构在Java中的应用实例

#### 2.3.1 使用树结构进行数据组织

树结构在Java中常被用于组织具有层级关系的数据，例如文件系统的目录结构、部门组织架构、抽象语法树（AST）等。

例如，文件系统可以使用树形结构来表示，其中每个节点代表一个文件或目录。Java中的`java.nio.file.FileTreeWalker`和`java.nio.file.FileVisitor`可以看作是树形遍历的应用实例。

#### 2.3.2 树结构在搜索引擎中的应用

在搜索引擎中，尤其是对于那些进行全文搜索和索引的搜索引擎，Trie树（前缀树）发挥着重要作用。Trie树可以帮助快速检索关键词前缀，并且可以方便地实现自动补全和拼写检查。

搜索引擎可能还使用了其他复杂的树形结构，如倒排索引，它将文档与关键词关联起来，帮助快速查找包含特定关键词的文档。

在本章节中，我们对Java树结构的基础进行了详细的学习，从理论到实践。我们了解了树的定义、属性，以及如何在Java中实现树形结构。我们还讨论了几种常见的树形结构，并探索了它们在真实世界应用中的实例。在下一章，我们将深入了解广度优先搜索（BFS）算法，并探讨其在树结构中的应用。

# 3. 广度优先搜索(BFS)算法详解

## 3.1 BFS算法的工作原理

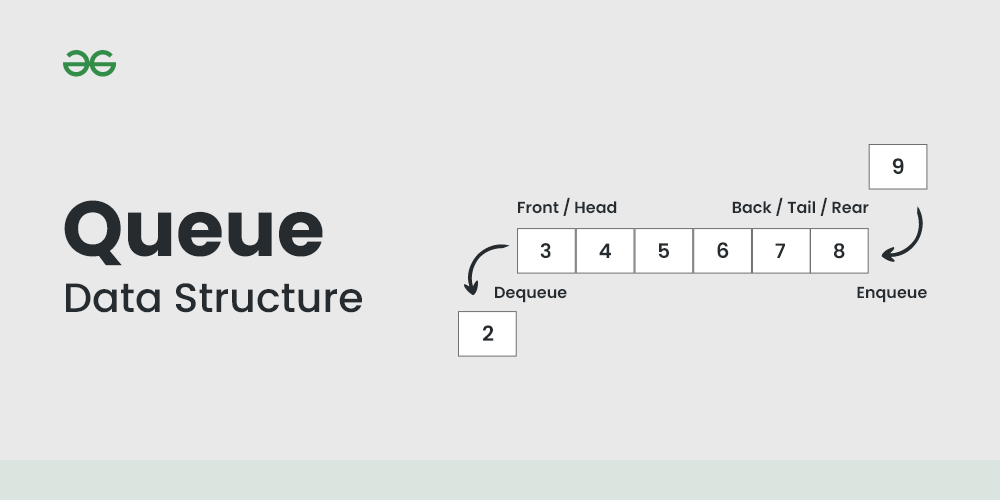
### 3.1.1 队列在BFS中的作用

BFS算法的核心是使用队列来追踪待访问的节点。队列是一种先进先出（FIFO）的数据结构，它在算法中扮演着至关重要的角色。在开始搜索之前，算法会将起始节点加入队列。然后，算法开始一个循环，在该循环中，它会不断地从队列中取出节点，并将其相邻且尚未访问的节点加入队列尾部。这个过程会一直持续，直到队列为空，即所有可达节点都被访问为止。

队列在BFS中的主要作用包括：

- **保持节点访问的顺序**：按照节点被发现的顺序将其加入队列，并在队列中保持这一顺序。
- **避免循环**：通过检查节点是否已在队列中，算法可以避免访问已经被访问过的节