Java中的并查集：树结构在群组管理中的应用案例

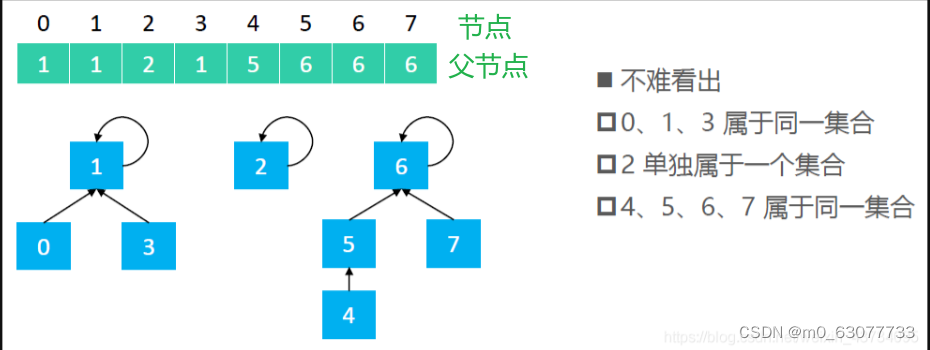
# 1. 并查集的基本概念与原理

## 1.1 并查集的定义
并查集是一种数据结构，用于处理一些不相交集合的合并及查询问题。它支持两种操作：
- `Find`: 确定某个元素属于哪一个子集，这可以用来确定两个元素是否存在于同一个子集中。
- `Union`: 将两个子集合并成一个集合。

## 1.2 应用场景
并查集广泛应用于图论中的问题解决，例如网络连接的检测，以及在其它领域如编译器的变量作用域管理等。它在处理动态连通性问题时表现出色，效率高，特别适合表示和解决这类问题。

## 1.3 并查集的特点
并查集的关键特性是它能够以几乎线性的时间复杂度执行操作。它之所以高效，是因为它的结构设计允许快速的查找和合并操作，同时它也很容易实现。其核心在于维护一种特殊的数据结构，使得元素间的连接关系可以高效更新和查询。

以上内容已经构成了一个连贯的介绍，接下来将会详细探讨并查集的数据结构实现。

# 2. 并查集的数据结构实现

## 2.1 并查集的数组表示方法

### 2.1.1 核心数据结构的定义

并查集是一种用来处理不相交集合的合并及查询问题的数据结构。其核心思想是让每个集合由一个代表元素来标识，通过每个元素直接或者间接指向其所在集合的代表。

在数组表示方法中，一个并查集可以用一个整数数组来实现。数组中的每个元素`parent[i]`表示元素`i`的父节点，对于非根节点，最终都会指向它所在集合的根节点。对于根节点，其父节点即为自身，即`parent[i] == i`。

以下是使用Python语言实现的并查集数据结构定义代码示例：

class UnionFind:
    def __init__(self, size):
        self.parent = [i for i in range(size)]  # 初始化时，每个节点自成一个集合，其父节点为自身

    def find(self, node):
        pass  # 查找操作将在下一小节详细介绍

    def union(self, node1, node2):
        pass  # 合并操作将在下一小节详细介绍

在这个类中，我们初始化了一个大小为`size`的数组`parent`，该数组将用于追踪每个节点的父节点。每个节点在开始时都指向自己，表示它们是各自集合的代表。

### 2.1.2 查找（Find）操作的实现

查找操作（`find`）的目的是找到一个元素所在的集合的代表（根节点）。查找操作需要递归或者循环遍历元素的父节点，直到找到根节点。

以下是查找操作的实现代码，以及逻辑分析：

class UnionFind:
    # ... (其它代码保持不变)

    def find(self, node):
        # 查找当前节点的根节点，并进行路径压缩优化
        if self.parent[node] != node:
            # 路径压缩：将当前节点直接指向根节点
            self.parent[node] = self.find(self.parent[node])
        return self.parent[node]

在上述代码中，我们首先检查当前节点是否是其所在集合的代表。如果不是，我们递归地调用`find`函数，直到找到根节点。路径压缩是通过将当前节点直接指向根节点来实现的，这极大地减少了后续查找操作的时间复杂度，使得其接近O(1)。

### 2.1.3 合并（Union）操作的实现

合并操作（`union`）的目的是将两个元素所在的集合合并成一个新的集合。合并操作通常涉及两个步骤：找到两个元素所在集合的根节点，然后让一个根节点指向另一个根节点。

以下是合并操作的实现代码，以及逻辑分析：

class UnionFind:
    # ... (其它代码保持不变)

    def union(self, node1, node2):
        # 合并两个节点所在的集合
        root1 = self.find(node1)
        root2 = self.find(node2)
        if root1 != root2:
            # 将一个根节点指向另一个根节点
            self.parent[root2] = root1

在这段代码中，我们首先找到两个元素的根节点。如果它们属于不同的集合（即它们的根节点不同），我们将一个根节点指向另一个根节点，从而完成合并。

## 2.2 并查集的路径压缩技术

### 2.2.1 路径压缩的基本思想

路径压缩是一种优化技术，用于加速并查集中查找操作的执行时间。在不使用路径压缩的情况下，查找操作的时间复杂度为O(logN)。而通过路径压缩，平均情况下的时间复杂度可以降低到接近O(1)。

基本思想是在执行查找操作时，将查找路径上的每个节点直接连接到根节点。这样在下一次查找操作时，就可以减少查找路径的长度，从而加快查找速度。

### 2.2.2 实践中的路径压缩方法

在代码实现中，路径压缩通常通过递归或循环的查找函数来实现。如上节代码示例所示，在查找操作中，我们找到根节点后，将路径上所有节点都连接到根节点。

### 2.2.3 路径压缩对性能的影响

路径压缩极大地改善了并查集的性能，尤其是在重复查询同一个元素所在集合的场景下。然而，路径压缩的优化效果与具体的使用场景紧密相关。在元素不频繁查找的情况下，路径压缩的效果可能不会那么明显。

路径压缩的平均时间复杂度分析通常涉及到随机化分析。在最坏的情况下，路径压缩的效果不会特别显著，但大多数情况下能显著降低时间复杂度。实际使用中，路径压缩后的并查集操作接近常数时间复杂度，因此在许多算法问题中，包括但不限于动态连通性问题、图的MST算法中，并查集被广泛使用。

## 2.3 并查集的启发式合并

### 2.3.1 启发式合并的原理

启发式合并，又称按秩合并或按大小合并，是一种优化策略，目的是降低合并操作导致的树的高度，从而进一步优化查找操作的效率。

### 2.3.2 合并规则的实现与优化

在实现启发式合并时，我们通常记录每个根节点所代表的集合的大小。合并操作时，我们比较两个集合的大小，并将较小集合的根节点连接到较大集合的根节点上。这样可以减少因合并操作导致树变高的可能性。

class UnionFind:
    # ... (其它代码保持不变)

    def union(self, node1, node2):
        root1 = self.find(node1)
        root2 = self.find(node2)
        if root1 != root2:
            # 启发式合并：将较小集合的根节点指向较大集合的根节点
            if self.rank[root1] > self.rank[root2]:
                self.parent[root2] = root1
            elif self.rank[root1] < self.rank[root2]:
                self.parent[root1] = root2
            else:
                self.parent[root2] = root1
                self.rank[root1] += 1

在这段代码中，`rank`数组记录了每个根节点所代表的集合的秩（高度）。在合并时，我们根据秩来决定哪个根节点指向另一个。这样能够尽