【AVL树详解】：Java中的高效平衡策略

# 1. AVL树的基本概念与特性

AVL树是一种自平衡的二叉搜索树，由Adelson-Velsky和Landis在1962年提出。这种树结构在每个节点处保持平衡因子（即左子树与右子树的高度差）的绝对值不超过1。AVL树的特性保证了最坏情况下查找、插入和删除操作的时间复杂度都维持在O(log n)。这种高效的数据结构广泛应用于需要快速查找和排序的场景中，比如数据库索引、内存管理等。下一章将详细介绍AVL树的理论基础，包括二叉搜索树的性质、AVL树的定义，以及如何通过旋转操作来维护树的平衡性。

# 2. AVL树的理论基础

### 2.1 二叉搜索树的性质与操作

#### 2.1.1 二叉搜索树的定义

在探索AVL树的理论基础之前，必须先理解二叉搜索树（BST）的概念。二叉搜索树是一种特殊类型的二叉树，它满足以下性质：对于树中的任意节点，其左子树上的所有节点的值都小于该节点的值，其右子树上的所有节点的值都大于该节点的值。这种特性使得二叉搜索树在进行查找、插入和删除操作时具有较高的效率。

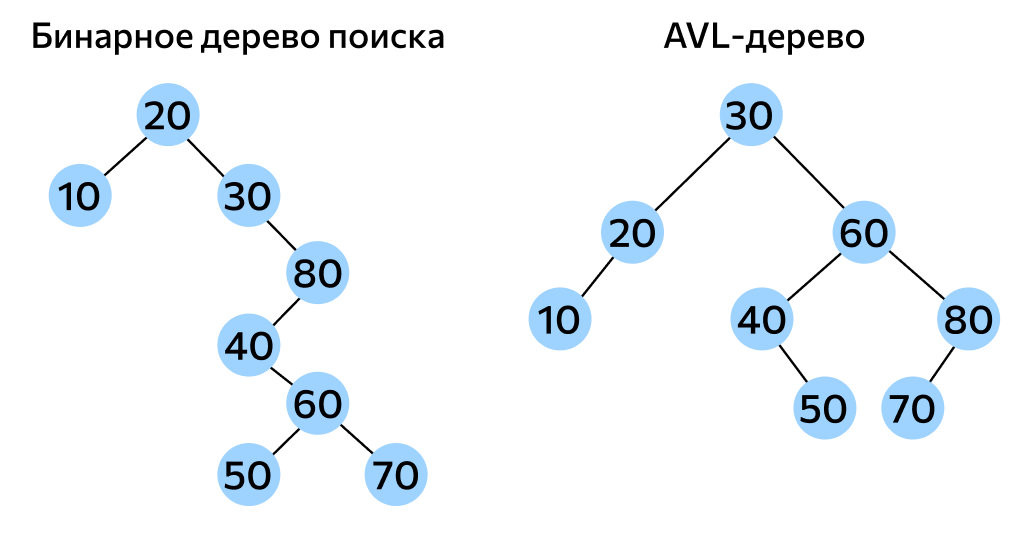
二叉搜索树的一个关键优势在于其有序性，这使得搜索操作可以采用类似于二分查找的策略，从而达到对数时间复杂度的效率。然而，若二叉搜索树的构造顺序不佳，它可能退化成一个链表，这样其性能就会下降到线性时间复杂度，这是AVL树需要解决的问题。

#### 2.1.2 插入、删除和查找操作

为了理解AVL树的工作原理，接下来我们详细探讨二叉搜索树的三种基本操作：

**查找操作**：从根节点开始，若目标值小于当前节点值，则在左子树中查找；若目标值大于当前节点值，则在右子树中查找；若相等，则找到目标值。这个过程会递归进行，直到找到目标值或叶子节点。

int search(Node node, int key) {
    if (node == null || node.value == key) {
        return node.value;
    }
    if (key < node.value) {
        return search(node.left, key);
    } else {
        return search(node.right, key);
    }
}

**插入操作**：插入操作类似于查找操作，只不过当到达一个空位置（叶子节点的子节点）时，创建一个新节点并将其插入。在插入后，需要检查树是否因为插入操作而失去了平衡。

**删除操作**：删除操作是最复杂的操作，需要考虑多种情况。若要删除的节点没有子节点，则直接删除；若有一个子节点，则用该子节点替换；若有两个子节点，则找到中序后继（或前驱），用它来替换要删除的节点，然后在子树中删除原来的中序后继节点。

### 2.2 平衡二叉树（AVL树）的定义

#### 2.2.1 AVL树的特点

AVL树是一种自平衡的二叉搜索树，它通过在每个节点处计算平衡因子（左右子树的高度差）来确保树的平衡性。AVL树的平衡因子只能是-1、0或1，任何节点不平衡都会通过旋转操作来调整。

在AVL树中，对树的任何修改都可能引起树的不平衡。这些修改包括插入新节点或删除节点。一旦检测到不平衡，就要进行旋转操作，以保证树的平衡性。

#### 2.2.2 平衡因子与平衡维护

平衡因子是AVL树中用于判断节点平衡度的关键值。对于任何节点，其平衡因子是其左子树的高度减去右子树的高度。为了维护AVL树的平衡性，节点的平衡因子必须在-1、0、1这三个值之一。如果一个节点的平衡因子超出这个范围，就需要进行旋转以恢复平衡。

旋转操作分为单旋转和双旋转。单旋转只涉及一个子节点，分为左旋和右旋。双旋转则涉及两个子节点，分为左右双旋和右左双旋。

### 2.3 AVL树的旋转操作

#### 2.3.1 单旋转和双旋转的原理

单旋转适用于插入或删除操作后产生的四种不平衡情况中的两种，具体来说就是：

- 右旋：当前节点的左子树比右子树高两个单位（例如，平衡因子是-2），此时需要对左子节点进行右旋。
- 左旋：当前节点的右子树比左子树高两个单位（例如，平衡因子是2），此时需要对右子节点进行左旋。

双旋转适用于其余两种不平衡情况，即：

- 右左双旋：先对左子节点的右子树进行左旋，然后再对该节点进行右旋。
- 左右双旋：先对右子节点的左子树进行右旋，然后再对该节点进行左旋。

#### 2.3.2 旋转对AVL树平衡的影响

旋转操作是保持AVL树平衡的关键。通过旋转，树的平衡因子可以回到允许的范围内，从而恢复树的平衡。旋转操作不仅调整了节点间的父子关系，而且也会改变某些节点的高度，这些变化将影响到平衡因子的计算。

正确执行旋转操作对于保持AVL树的性能至关重要。因为每次插入或删除后都可能导致树的重新平衡，所以高效的旋转操作是必要的，它确保了AVL树在每次修改后仍然保持对数级的查找效率。

graph TD;
    A(平衡因子)
    B[不平衡] -->|左旋| C[左子树过高]
    B -->|右旋| D[右子树过高]
    C -->|右左双旋| E[左子树的右子树过高]
    D -->|左右双旋| F[右子树的左子树过高]
    E --> G[恢复平衡]
    F --> G

在上述的mermaid流程图中，我们可以看到不平衡的情况是如何通过旋转得到调整，最终达到平衡状态的。每一次旋转都是为了恢复AVL树的平衡性，保证其高效运行。

在实现AVL树时，需要在每次插入或删除节点后检查每个节点的平衡因子，以及相应地调整树的结构。通过代码逻辑和执行顺序的严格控制，AVL树能够在动态数据中保持其优越的性能。

以上内容详细介绍了AVL树的理论基础，从二叉搜索树的概念出发，深入到AVL树的自平衡机制，以及为了保持平衡所进行的旋转操作。这些内容构成了理解AVL树的关键知识体系，并为后面章节中AVL树在Java中的实现打下坚实的理论基础。

# 3. AVL树在Java中的实现

## 3.1 AVL树节点类的设计
### 3.1.1 节点类的属性和构造方法

在Java中实现AVL树，首先需要定义节点类。AVL树的节点类需要包含数据域、指向左右子树的引用以及一个用于记录节点平衡因子的属性。平衡因子通常是指节点左子树的高度减去右子树的高度。

class AVLNode {
    int key;             // 节点存储的数据
    int height;          // 节点的高度
    AVLNode left;        // 左子树
    AVLNode right;       // 右子树

    // 构造方法，初始化节点的高度为1（假设新节点是叶节点）
    AVLNode(int d) {
        key = d;
        height = 1;
    }
}

在上述代码中，`AVLNode` 类包含了四个属性：`key` 表示存储的数据，`height` 表示节点的高度，`left` 和 `right` 分别表示指向左右子树的指针。构造方法用于创建一个新节点，初始高度设置为1，表示这是一个叶节点。

### 3.1.2 平衡因子的计算与更新

AVL树的平衡因子对于保持树的平衡至关重要。计算平衡因子的逻辑很简单，就是左右子树高度的差值。

int getBalance(AVLNode node) {
    if (node == null)
        return 0;
    return height(node.left) - height(node.right);
}

在上述代码中，`getBalance` 方法接受一个 `AVLNode` 类型的参数，并返回这个节点的平衡因子。`height` 方法是一个辅助方法，用于计算传入节点的高度，如果节点为 `null