网络流算法深入解析：Ford-Fulkerson、Edmonds-Karp与Dinic

"这篇文档详细介绍了网络流算法，包括Ford-Fulkerson算法、Edmonds-Karp算法和Dinic算法，并提供了具体的图例帮助理解。网络流算法在解决匹配问题、Hall婚姻定理等实际问题中有着广泛应用。文章没有涉及预留推进算法，因为它证明较为复杂，但建议感兴趣的人查阅《算法导论》。" 网络流算法是图论中的一个重要概念，它在处理网络中的流量分配问题时非常有用。最大流问题旨在寻找在网络中从源点到汇点的最大可能流量，而最小割问题则是找出分割网络使得源点一侧的节点无法向汇点传递更多流量的最小边集合。这两个问题通过最大流最小割定理相互关联。 首先，Ford-Fulkerson算法是一种迭代寻找增广路径的方法来逐步增加流的总量，直到无法再找到增广路径为止。在每次迭代中，算法会选取一条从源点到汇点的增广路径，以路径上最小的剩余容量作为流的增量，并更新所有边的剩余容量。该算法的时间复杂度为O(VE^2)，其中V是顶点数量，E是边的数量。 接着，Edmonds-Karp算法是Ford-Fulkerson算法的一种优化版本，它固定了增广路径的查找策略，即总是选择具有最短路径的增广路径。这种策略确保了算法的运行时间不超过O(VE^2)，但在实际问题中往往能更快地找到最大流，因为短路径通常意味着更多的增广机会。 Dinic算法则使用层次队列来更高效地寻找增广路径，其时间复杂度为O(V^2E)，虽然在最坏情况下比Ford-Fulkerson稍慢，但在很多情况下性能更优，特别是在稠密图中。Dinic算法通过多阶段层次搜索来找到增广路径，每个阶段尽可能地将流量从源点推送至尽可能接近汇点的节点。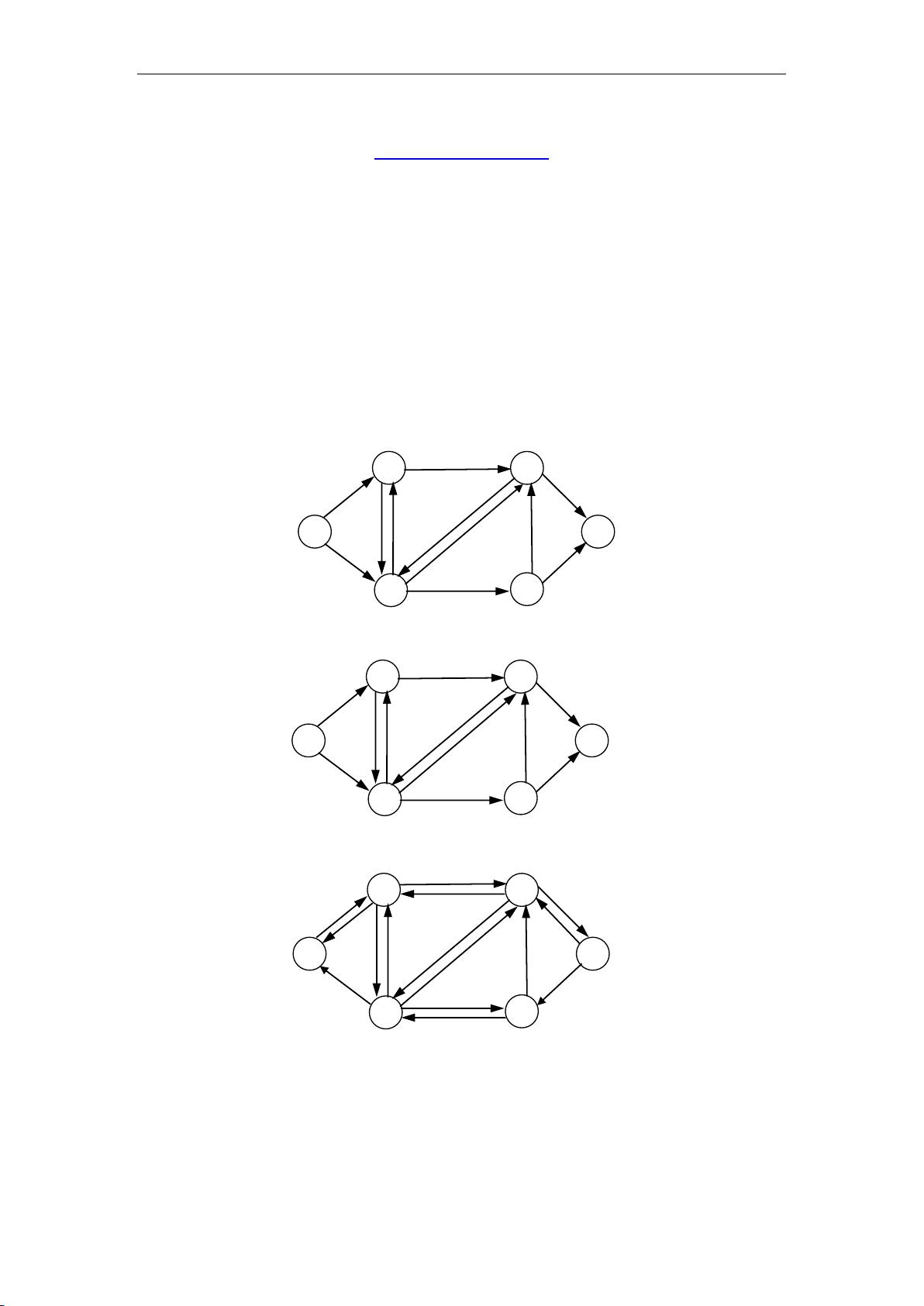 通过图例，我们可以看到网络流如何在实际问题中体现，例如图1展示了网络中的边和容量，图2展示了流量的分配，图3展示了由流量分配后的剩余网络。图4和图5进一步解释了在寻找增广路径和确定流增量的过程。 总结来说，网络流算法是一组强大的工具，能够解决各种流量分配问题，从简单的管道输水问题到复杂的匹配问题。Ford-Fulkerson、Edmonds-Karp和Dinic算法是解决这些问题的关键方法，它们各有特点，适用于不同类型的网络结构。理解并掌握这些算法，对于解决实际的计算问题至关重要。