Dijkstra算法详解与复杂性分析

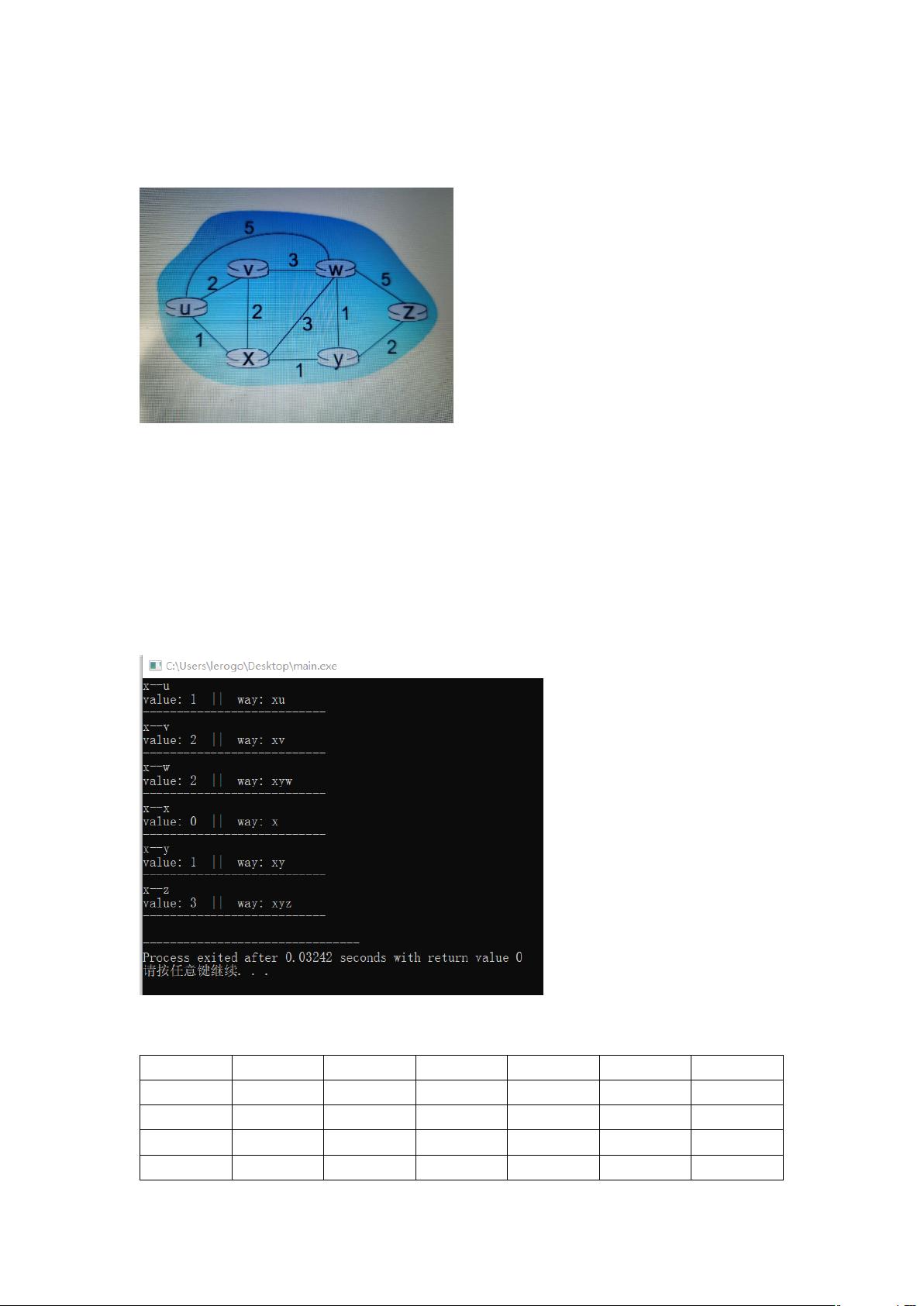
"该资源是一份关于计算从特定路由器X出发到其他路由器最短路径的作业，涉及到Dijkstra算法的应用及分析，同时讨论了网络拥塞的问题和拥塞控制的触发条件。" 在这个问题中，我们首先面临的是一个路由网络的问题，其中X路由器需要找到到所有其他路由器的最短路径。这个问题可以通过应用Dijkstra算法来解决，这是一种著名的用于找出图中两点间最短路径的算法。Dijkstra算法的核心思想是从一个起点开始，逐步扩展最短路径，直到达到所有目标点。 在Dijkstra算法的实施过程中，我们首先初始化数据，定义集合N（已知最短路径的点，初始包含起点X）和集合U（未处理的点）。对于任意两点x和y，C(x,y)表示它们之间的路径成本，如果两点之间无法直接连接，则成本记为无穷大。同时，D(x)记录点x到起点X的最短距离，Dway(x)记录从X到x的具体路径。 算法的执行包括以下步骤： 1. 从集合U中选择距离最小的点p，将其加入N集合，并更新与p相邻节点的最短距离和路径。 2. 重复此过程，直到集合U为空，即所有点都被处理过。 根据题目描述，还给出了一个C++代码实现的暗示，但具体内容并未给出。通常，Dijkstra算法的实现会涉及优先队列（如二叉堆）来高效地选取当前距离最小的点。 接下来，讨论了Dijkstra算法的复杂性和问题。在最坏的情况下，算法的时间复杂度为O(n^2)，因为它需要检查每个节点与其他所有节点的连接。这在路由器数量巨大的网络中可能会导致效率低下。此外，由于算法基于局部最优决策，可能存在“振荡”现象，即路径在不同的迭代中反复变化，可能导致网络拥塞和不稳定。 网络拥塞通常发生在路由器无法处理当前流量负载时，例如输入线路的分组太多，超过了路由器的处理能力或内存容量。而拥塞控制是为了避免这种情况，通过调整发送方的数据速率，确保网络不会过度饱和。拥塞控制可以是全局的，涉及到网络中的多个节点，或者端到端的，由源和目的地之间的通信端点协作进行。 在本例中，网络拥塞可能因路由器处理器速度不足、内存容量限制，或者因路由决策导致的反向流量增加而触发。拥塞控制则通过探测网络状况并相应调整发送速率来预防或缓解这些问题，以保持网络的稳定运行。