MATLAB绘制控制系统根轨迹分析
72 浏览量
更新于2024-06-27
收藏 1.07MB PPT 举报
"该资源是一个关于使用MATLAB绘制根轨迹的PPT课件,主要讲解了如何通过根轨迹分析控制系统的稳定性以及如何进行系统校正。"
本文将深入探讨根轨迹分析法及其在MATLAB中的应用,特别是针对给定的开环系统传递函数的案例分析。根轨迹分析是控制系统设计和稳定性研究的重要工具,它允许我们了解参数变化对闭环系统性能的影响,并据此优化系统参数。
首先,根轨迹是系统闭环特征方程的根在复平面上的轨迹,当系统的开环增益发生变化时,这些根会沿着特定路径移动。通过绘制根轨迹,我们可以观察到随着增益的变化,闭环系统的极点如何移动,从而分析系统的动态性能和稳定性。
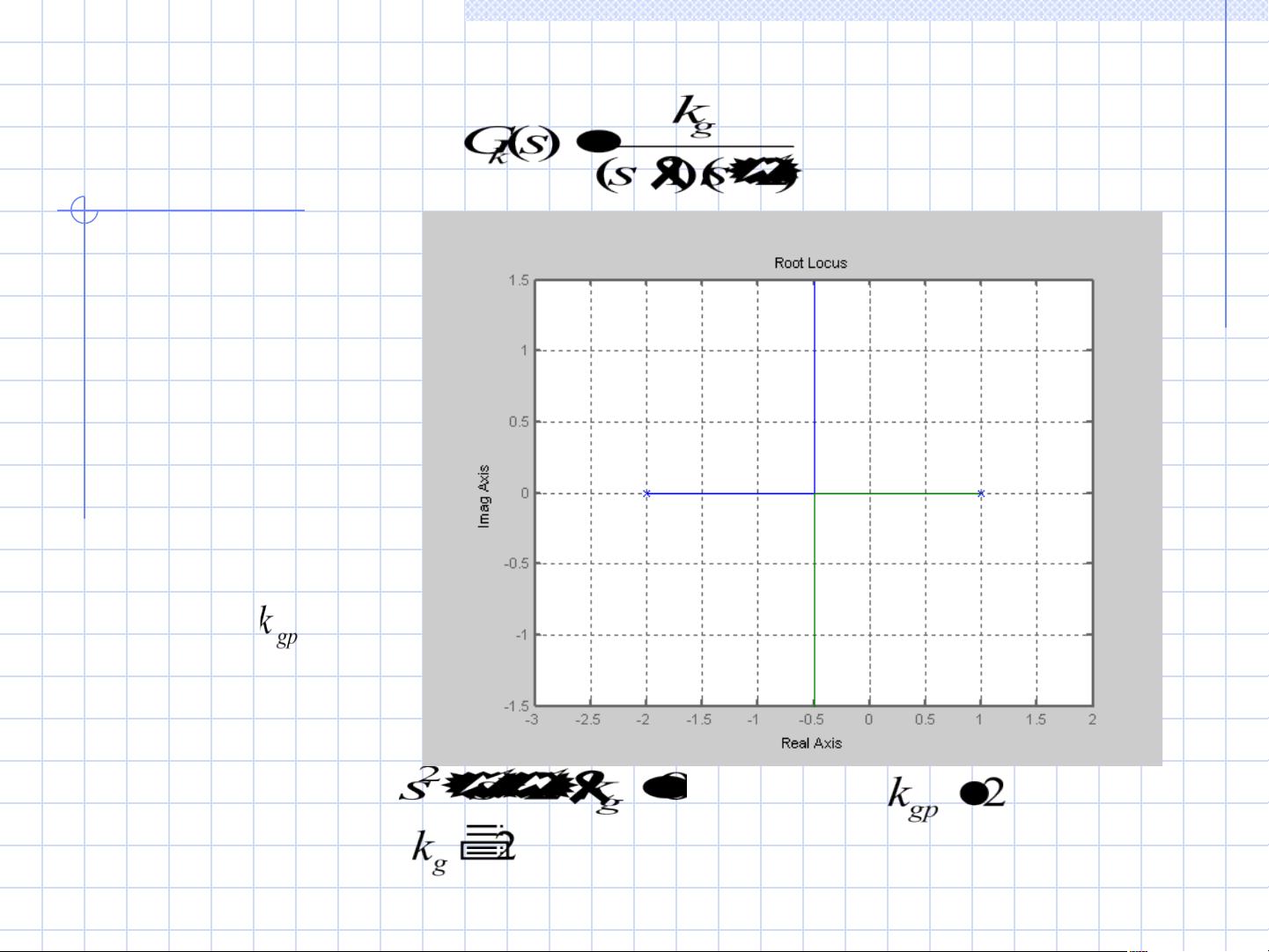
在描述的案例中,给定的开环系统传递函数为:
\[ G(s) = \frac{k}{(s+4)(s+6)(s^2 + 4s + 7)(s^2 + 9s + 14)} \]
案例要求绘制根轨迹并确定使闭环系统稳定的增益k的取值范围。我们首先确定开环系统的极点和零点,然后利用根轨迹的几何规则,如实轴上的根轨迹区间、渐近线、分离角、入射角等来绘制轨迹。
实轴上的根轨迹区间由开环极点决定,这里为[-4, 0)和(6, +∞)。渐近线与实轴的交点为[-3, -2],倾角计算可以帮助我们确定根轨迹在这些点的倾斜情况。分离角(点)是根轨迹与实轴相交的角度,对于这个例子,我们可以近似找到分离点的位置。入射角是根轨迹与虚轴的夹角,对于稳定性分析至关重要。
在MATLAB中,可以使用`rlocus`函数绘制根轨迹图,它会自动计算并显示根轨迹,同时给出稳定性边界。通过分析根轨迹图,我们可以找出使系统稳定的k值范围,即所有闭环极点必须位于s平面的左半平面。
在案例中,通过计算和分析,发现最大增益k约为9.375时,对应的根轨迹点位于s=-2.5,这是近似分离点。入射角的计算帮助我们更准确地理解根轨迹的运动,而与虚轴的交点则提供了关于系统响应速度的信息。
此外,通过分析根轨迹,还可以推导出系统校正的方法,比如串联或反馈校正,以改善系统的稳定性和性能指标。在MATLAB中,可以结合其他控制设计工具,如PID控制器设计或频率域分析,进一步优化系统。
根轨迹分析是控制系统设计的关键步骤,它为我们提供了一种直观的方式去理解和调整系统性能。通过MATLAB这样的软件工具,我们可以方便地实现根轨迹的绘制和分析,从而更好地理解和优化控制系统。
111 浏览量
200 浏览量
242 浏览量
185 浏览量
841 浏览量
2021-09-15 上传
2021-10-10 上传
2021-10-09 上传
2022-11-02 上传
xinkai1688
- 粉丝: 397
最新资源
- Python编程基础视频课件精讲
- FairyGUI-unreal:掌握Unreal Engine的高效UI设计
- C++实现Excel基本操作教程
- 实时聊天小部件的Python实现与Pusher Channels集成
- Android版本比较工具库:轻量级字符串比较方法
- OpenGL基础教程:编译顶点着色器与片段着色器
- 单片机实现的24小时制电子定时器设计
- ThinkPHP 3.1.2框架中文开发手册全解
- 离散数学第七版习题解答:奇偶数题答案解析
- 制造行业素材资源压缩包分享
- C#编程实现打印与测试程序详解
- Konveyor:快速生成Android随机数据类库
- 掌握Symfony集合:使用Vanilla JS实现高效表单管理
- Spring Boot MVC模板项目:快速启动Spring MVC与嵌入式Jetty
- 最新metro风格VB在线升级程序源码分享
- Android开发入门实践:新手指南与实践技巧