粒子群优化算法解析与MATLAB实现

"基本粒子群算法的matlab实现" 粒子群优化算法（Particle Swarm Optimization, PSO）是一种基于群体智能的优化技术，源自对复杂适应系统（CAS）的研究，特别是对鸟群觅食行为的模拟。该算法由Eberhart和Kennedy在1995年首次提出，它在解决多维度连续优化问题时展现出强大的能力。 在PSO算法中，每一个优化问题的可能解被看作是一个“粒子”，这些粒子存在于一个d维的搜索空间内。每个粒子都有一个位置和速度，它们共同决定了粒子在搜索空间中的移动方式。粒子的目标是寻找最优解，这对应于最高适应值或最低目标函数值。每个粒子的适应值是根据目标函数计算得出的，而粒子的速度则受到两个关键因素的影响：一是粒子自身的最佳位置（个人最佳，pBest），二是整个群体的最佳位置（全局最佳，gBest）。粒子会根据这两个最佳位置调整其飞行方向和速度，以更接近最优解。 具体来说，粒子的速度更新公式通常如下： \[ v_{id} = w \cdot v_{id} + c_1 \cdot r_1 \cdot (pBest_{id} - x_{id}) + c_2 \cdot r_2 \cdot (gBest_i - x_{id}) \] 其中，\(v_{id}\) 是第i个粒子的d维速度向量的第d个分量，\(x_{id}\) 是粒子的当前位置，\(pBest_{id}\) 和 \(gBest_i\) 分别是粒子的个人最佳位置和全局最佳位置，\(w\) 是惯性权重，\(c_1\) 和 \(c_2\) 是加速常数，\(r_1\) 和 \(r_2\) 是两个在0到1之间的随机数。这个公式反映了粒子在保持现有速度（惯性权重）的同时，受到个人经验和群体智慧的双重影响。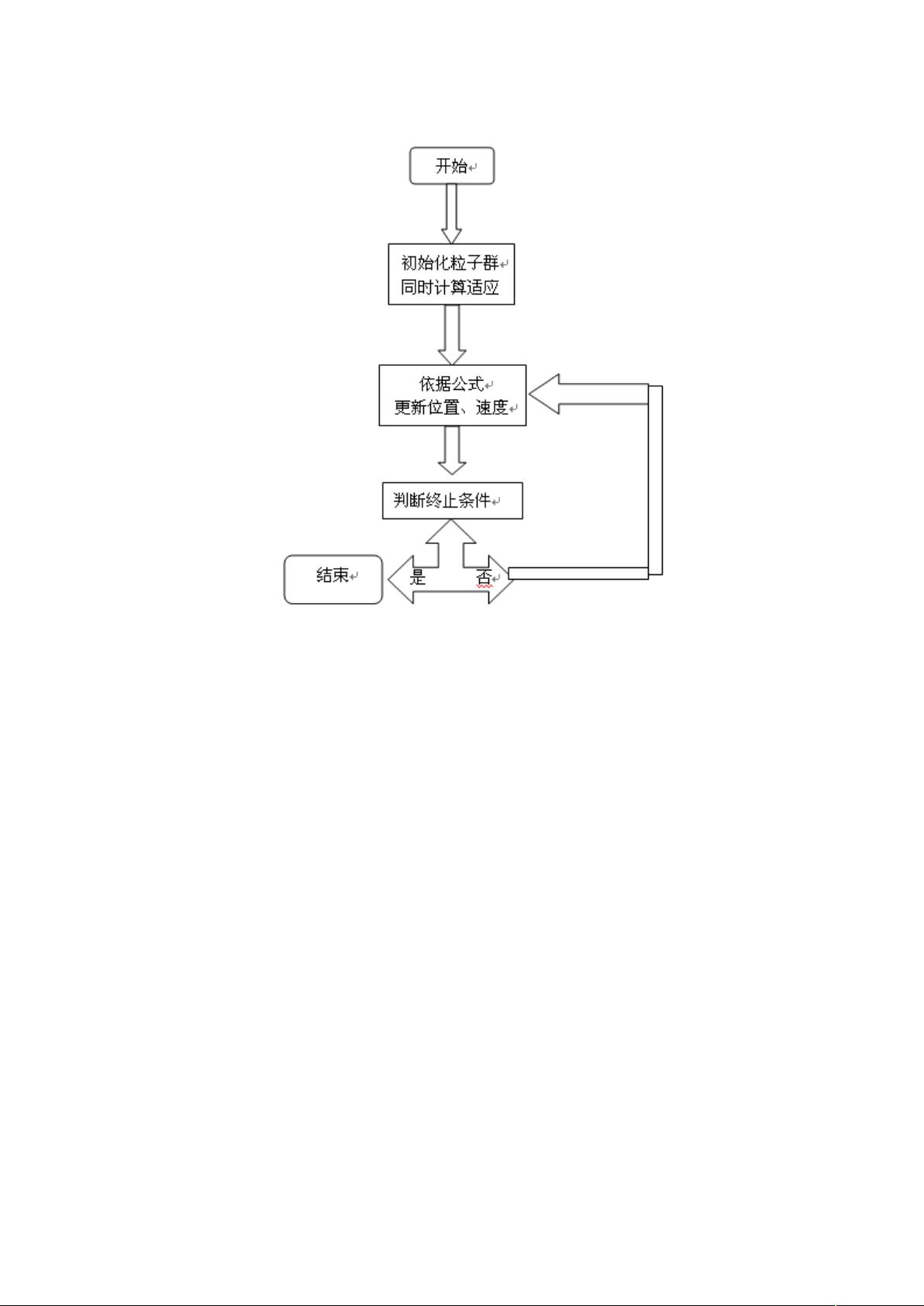 在MATLAB中实现PSO算法，一般包括以下几个步骤： 1. 初始化：随机生成粒子群的位置和速度。 2. 计算适应值：根据目标函数评估每个粒子的位置。 3. 更新个人最佳和全局最佳：如果粒子的新位置比以前更好，则更新个人最佳；同时比较所有粒子的个人最佳，更新全局最佳。 4. 更新速度和位置：根据上述速度更新公式计算新的速度和位置。 5. 循环迭代：重复步骤2至4，直到满足停止条件（如达到最大迭代次数、适应值满足精度要求等）。 MATLAB代码实现时，可以利用循环结构实现算法流程，结合MATLAB的随机数生成功能和向量化操作，以提高效率。同时，为了防止算法陷入局部最优，可以通过调整惯性权重、加速常数以及随机性参数来平衡探索和开发。 总结起来，PSO算法是一种借鉴生物群体行为的全局优化方法，具有简单易实现、鲁棒性强的特点。在MATLAB中，通过合理的编程技巧，可以有效地应用PSO解决各种优化问题。然而，理解和调整算法参数对于优化性能至关重要，如惯性权重的退减策略、加速常数的选择等，都需要根据具体问题进行适当调整。