因子分析步骤与公因子计算详解

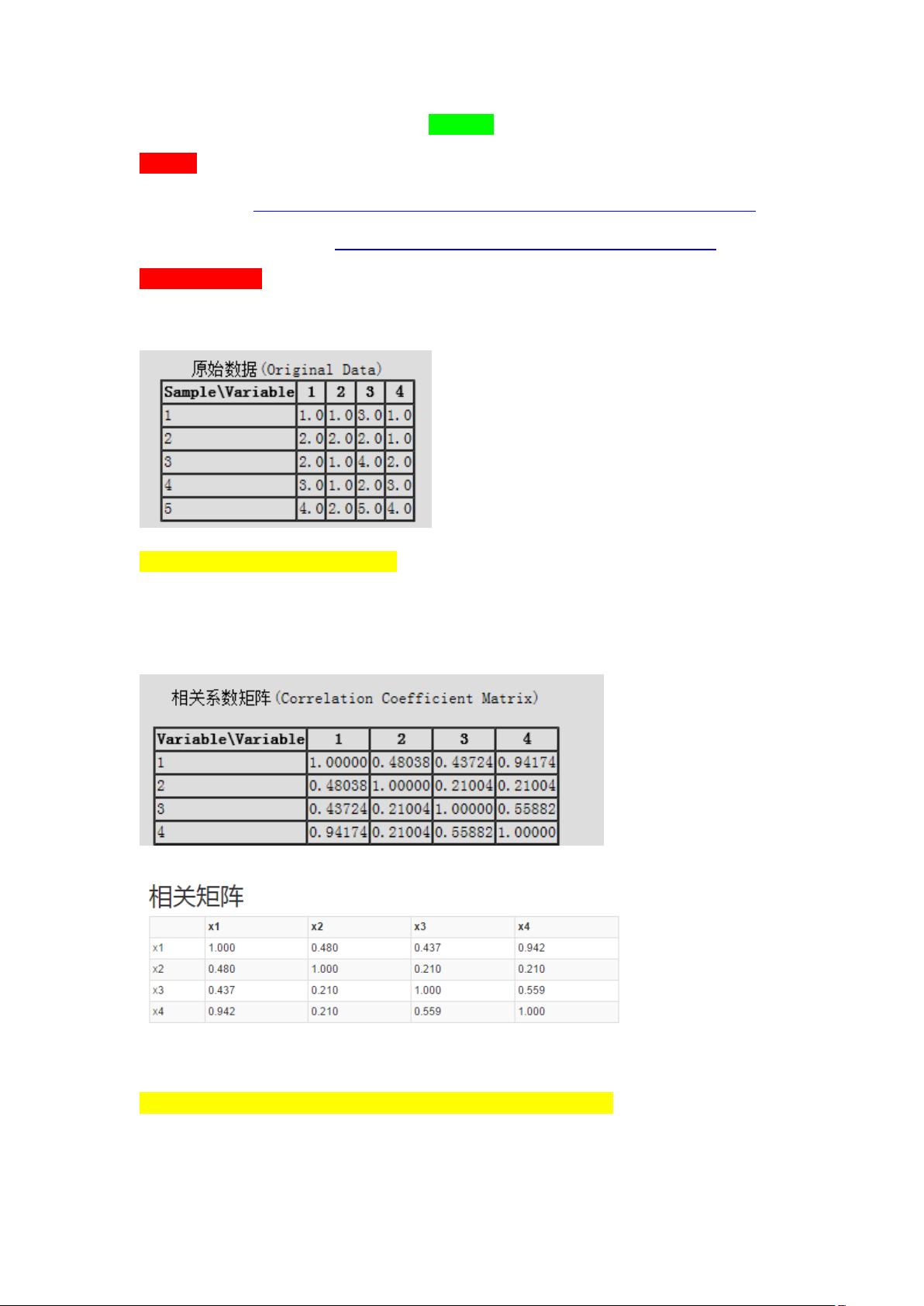
这篇资源主要介绍了因子分析的基本概念和步骤，提供了相关的教学材料链接以及一个具体的因子分析案例。因子分析是一种统计方法，用于发现变量间隐藏的结构关系，通过减少数据的维度来简化数据分析。它主要涉及到矩阵运算、特征值与特征向量计算、因子载荷矩阵、公因子方差表、正交旋转以及因子得分的计算。 1. 因子分析的步骤： - 计算相关矩阵R：基于原始数据，计算变量间的相关性，形成相关系数矩阵。 - 求解特征值和特征向量：对相关矩阵R进行特征分解，得到特征值和对应的特征向量，它们反映了各因子的影响力大小和方向。 - 确定因子个数：根据研究目的或特定准则（如Kaiser-Guttman法则，特征值大于1作为选取标准）决定提取的因子个数。 - 计算因子载荷矩阵：选取的特征向量乘以对应的平方根特征值，得到因子载荷矩阵，它描述了每个变量与因子的关系强度。 - 公因子方差表：计算因子载荷矩阵每一行的平方和，得到公因子方差，反映因子解释的总变异程度。 - 方差极大正交旋转：通过正交旋转，使因子载荷矩阵更加简单明了，便于解释，提高因子的可解释性。 - 正交因子得分：利用正规化后的数据矩阵X，结合方差极大正交矩阵A的转置和相关系数矩阵R的逆，计算得到因子得分，这些得分可以作为新变量用于后续分析。 2. 相关软件/插件： - 提供了一个在线教程链接，可能是一个教学平台，包含因子分析的详细讲解和实例。 - 另一个链接指向一个因子分析程序，可能是用于实际操作的工具，允许用户输入数据并执行因子分析。 3. 具体计算过程： - 特征值和特征向量的计算：这是基础的线性代数运算，用于找出矩阵的主要特性。 - 方差极大正交旋转：通过优化算法，寻找使得因子载荷矩阵各因子之间差异最大的旋转角度，通常采用Varimax旋转方法。 - 正交因子得分计算：运用线性代换公式，将原始数据转换为因子得分，便于进一步的分析和解释。 因子分析是统计建模中常用的数据降维技术，对于理解和揭示变量之间的复杂关系非常有用。在社会科学、市场研究、心理学等领域有着广泛的应用。正确理解和运用因子分析能够帮助研究者更有效地处理大量数据，提炼出关键信息。