MATLAB实现：灰度图缩放的最近邻与双线性插值算法

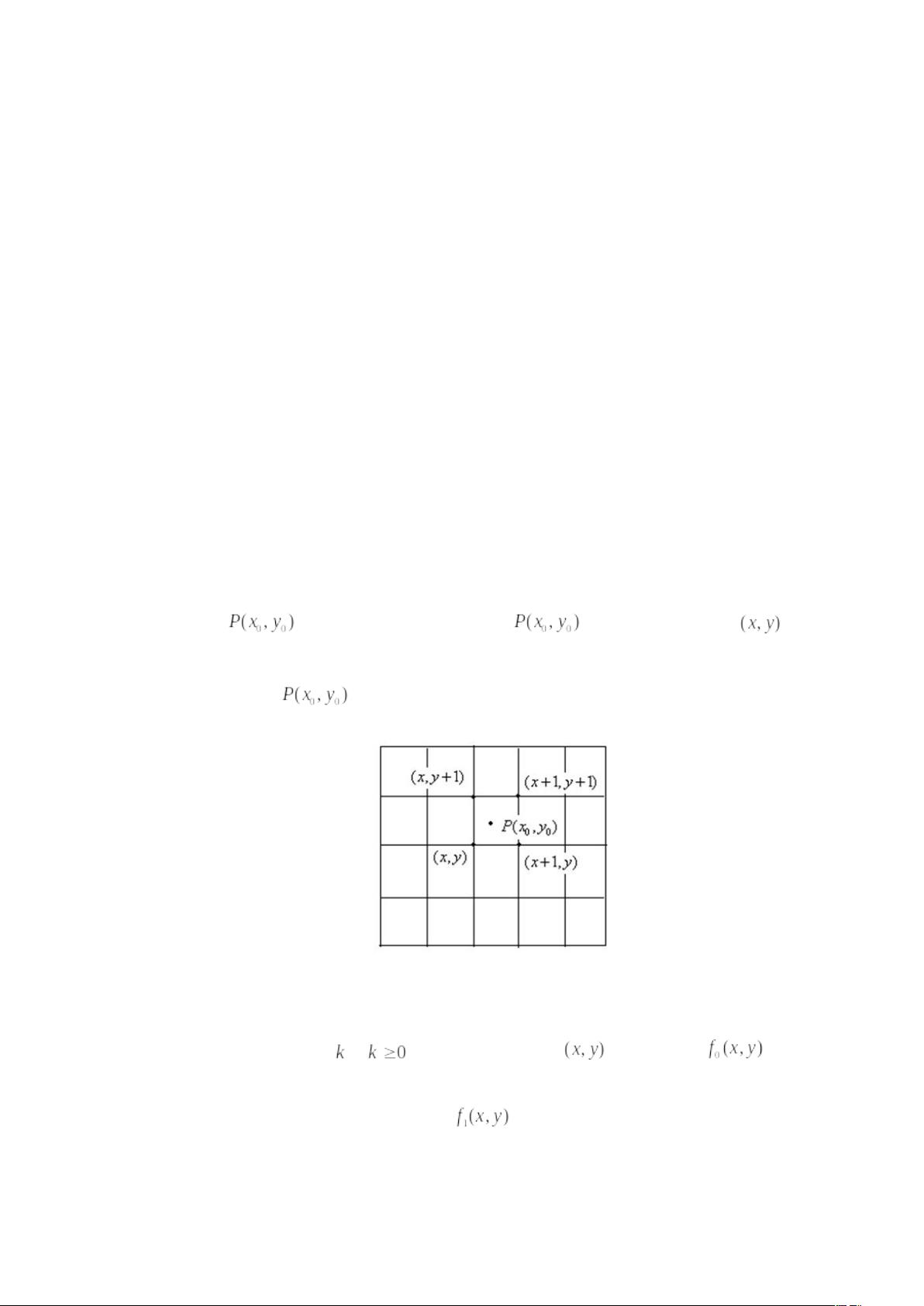
"本文主要介绍了如何在MATLAB环境下利用最近邻算法和双线性插值算法对灰度图像进行缩放。这两种算法是图像处理中常见的插值方法，用于提高图像缩放时的画质。" 最近邻算法（Nearest Neighbor Interpolation）是一种基本的图像缩放方法，它的原理是对非整数坐标点的灰度值进行四舍五入，直接取最近的整数坐标点的灰度值作为该点的近似值。这种方法简单快速，但可能会导致缩放后的图像出现像素化的现象，边缘不平滑。在MATLAB中实现最近邻插值算法，首先读取图像，确定缩放比例，创建相应大小的新矩阵，然后遍历新矩阵的每个元素，通过四舍五入获取源图像中对应的整数坐标点的灰度值，并将其赋值给新矩阵。 双线性插值算法（Bilinear Interpolation）相对复杂，它通过对目标点周围的4个最近邻点进行两次线性插值来计算出新的灰度值，从而提供更平滑的图像缩放效果。在MATLAB中实现双线性插值，同样需要读取图像并确定缩放比例，然后对每个新坐标点进行两次线性插值运算，分别计算出横轴和纵轴方向上的插值，再结合这两个结果得到最终的灰度值。这种方法虽然提高了图像质量，但计算量较大，耗时较长。 在给出的代码示例中，MATLAB程序首先使用`imread`函数读取名为'lena.jpg'的图像，然后通过用户输入的缩放因子k确定缩放比例。对于最近邻算法，程序通过`ceil`函数取整并用`for`循环将源图像的每个像素复制到新图像对应位置。对于双线性插值部分，代码未给出完整的实现，但通常会涉及对每个新坐标点的四个邻接点进行线性插值计算。 总结起来，最近邻算法适用于快速缩放，但图像质量可能较差，而双线性插值算法则能够提供更好的视觉效果，但计算成本较高。在实际应用中，选择哪种算法取决于对速度和质量的需求平衡。MATLAB提供了方便的工具和函数支持这些图像处理操作，使得图像缩放的实现变得简单易行。