MATLAB中的PID控制器设计与Ziegler-Nichols整定

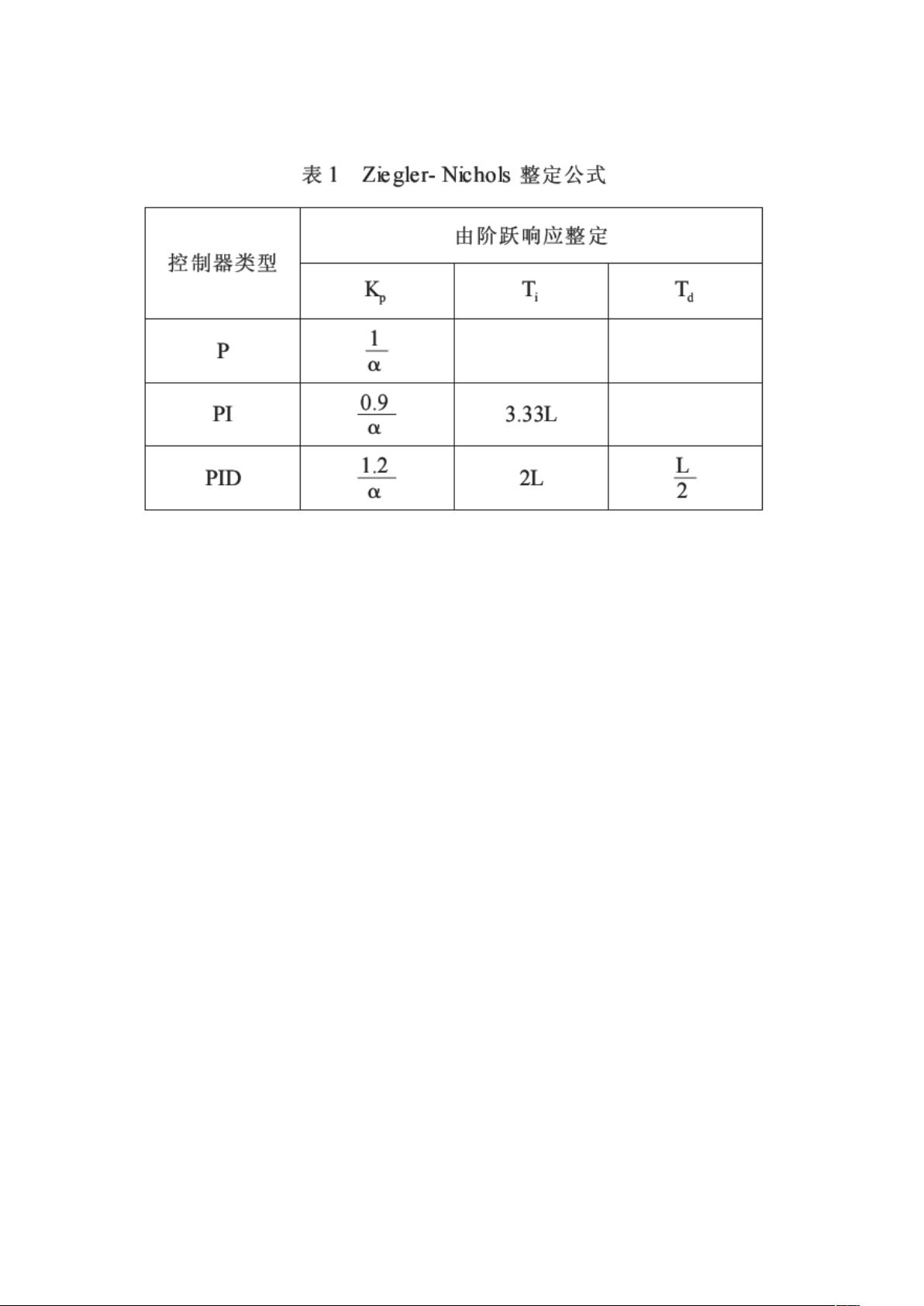
"这篇文档是关于使用MATLAB进行PID控制器设计的实验报告，作者通过介绍PID控制的基本原理，Ziegler-Nichols参数整定方法，并展示了如何在MATLAB环境下进行PID控制器的设计与仿真。" 文章详细内容: PID控制器是一种广泛应用的反馈控制策略，其优势在于不需要精确的系统模型，只需通过比例、积分和微分作用来调整控制信号，从而有效地减少稳态误差并提高系统性能。PID控制器的三个主要参数——比例系数(Kp)、积分系数(Ti)和微分系数(Td)的选择对系统性能有直接影响。 在PID控制中，控制器对误差信号进行比例运算可以迅速响应变化，积分作用能消除稳态误差，而微分作用则有助于改善系统的动态响应，但微分项可能对系统稳定性产生负面影响，特别是对高频干扰敏感。 Ziegler-Nichols参数整定法是一种常用的PID控制器参数设定方法，尤其适用于一阶或接近一阶的对象模型。该方法通过对象的阶跃响应曲线来确定控制器参数，比如对象模型的增益K、时间常数T和滞后时间L。在MATLAB中，可以使用`step()`函数获取开环阶跃响应曲线，或者使用`dcgain()`函数直接计算对象模型的直流增益K。 在MATLAB环境下，设计PID控制器通常包括以下步骤： 1. 定义被控对象的模型，这可能是通过实验数据或理论建模得到的。 2. 应用Ziegler-Nichols法则，根据对象模型的参数计算初始的PID控制器参数。 3. 使用MATLAB的Simulink工具箱构建系统模型，包括被控对象和PID控制器。 4. 仿真系统行为，分析控制性能，如超调、上升时间和稳态误差等。 5. 根据仿真结果调整PID参数，迭代优化直至获得满意的控制性能。 通过不断的参数调整和仿真，可以找到最优的PID控制器参数，使得控制系统达到预期的性能指标。MATLAB提供的工具和算法大大简化了这一过程，使得工程师能够快速有效地设计和优化PID控制器，适应各种复杂控制任务的需求。