快速傅里叶变换与信号处理：线性代数新篇章

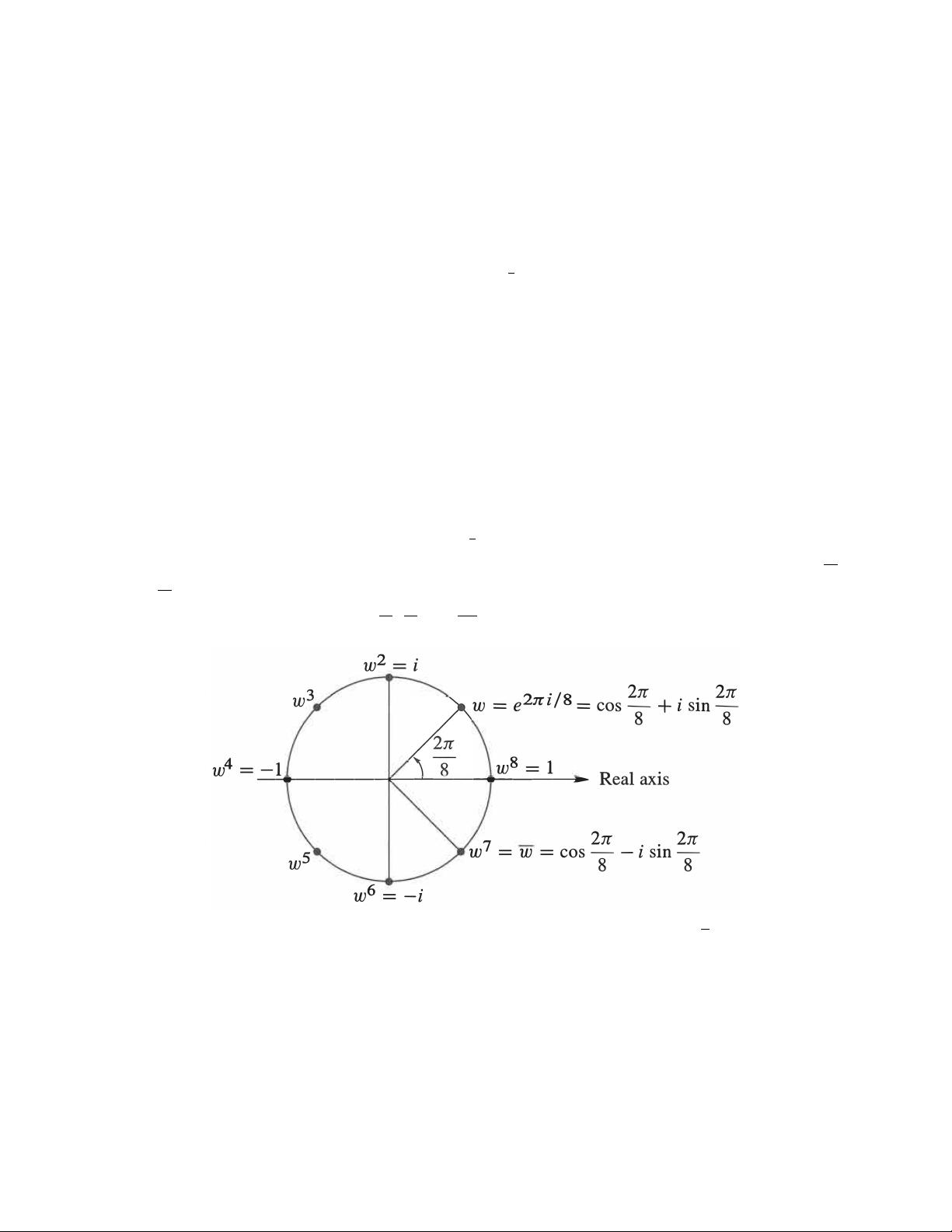
"中文翻译Introduction to Linear Algebra, 5th Edition 9.3节" 这篇摘要主要介绍了线性代数中的一个重要应用，即快速傅里叶变换（FFT），它在信号处理和其他领域有着广泛的应用。线性代数通常涉及理论的深度讲解，但本节专门讨论了一个实用的数值算法，即FFT，它是上个世纪最具影响力的计算技术之一。 快速傅里叶变换是一种高效计算傅里叶变换的方法。傅里叶变换是数学中的一种工具，能够将一个函数从其原始的“时域”或“空间域”表示转换到“频域”表示。这种转换对于分析周期性或近似周期性的信号至关重要。在传统的傅里叶乘法中，计算n×n的傅里叶矩阵和其逆矩阵需要n²次乘法，而FFT则将这个复杂度降低到n乘以12 log2 n次乘法，极大地提高了计算效率。 FFT的实现依赖于单位根的概念。单位根是解复数方程zn=1的特殊复数解，这些解在复平面上均匀分布在单位圆上。例如，z8=1的8个解形成了45度间隔的点。一个重要的单位根是w=eiθ，其中θ是角度，例如在8次方程中，θ=2π/8。通过使用单位根的幂，可以有效地对傅里叶矩阵进行操作，从而实现FFT。 FFT不仅改变了信号处理的面貌，还催生了整个行业的快速发展，特别是对电气工程师而言，傅里叶变换已成为他们的基本工具。通过FFT，工程师可以更便捷地分析和处理各种信号，如音频、图像和通信信号等。 在实际应用中，FFT的思想可以用于降维计算，例如从8×8的傅里叶矩阵简化到4×4矩阵，再进一步简化到更小的矩阵。这种分治策略使得对大尺寸矩阵的处理变得更加高效，例如在计算F1024时，通过一系列降维和升维操作，大大减少了所需的乘法次数，从而实现了快速计算。 9.3节的内容强调了快速傅里叶变换在理论与实践之间的桥梁作用，以及它在处理大规模数据时的计算优势。理解并掌握FFT是现代工程和科学计算中的必备技能。