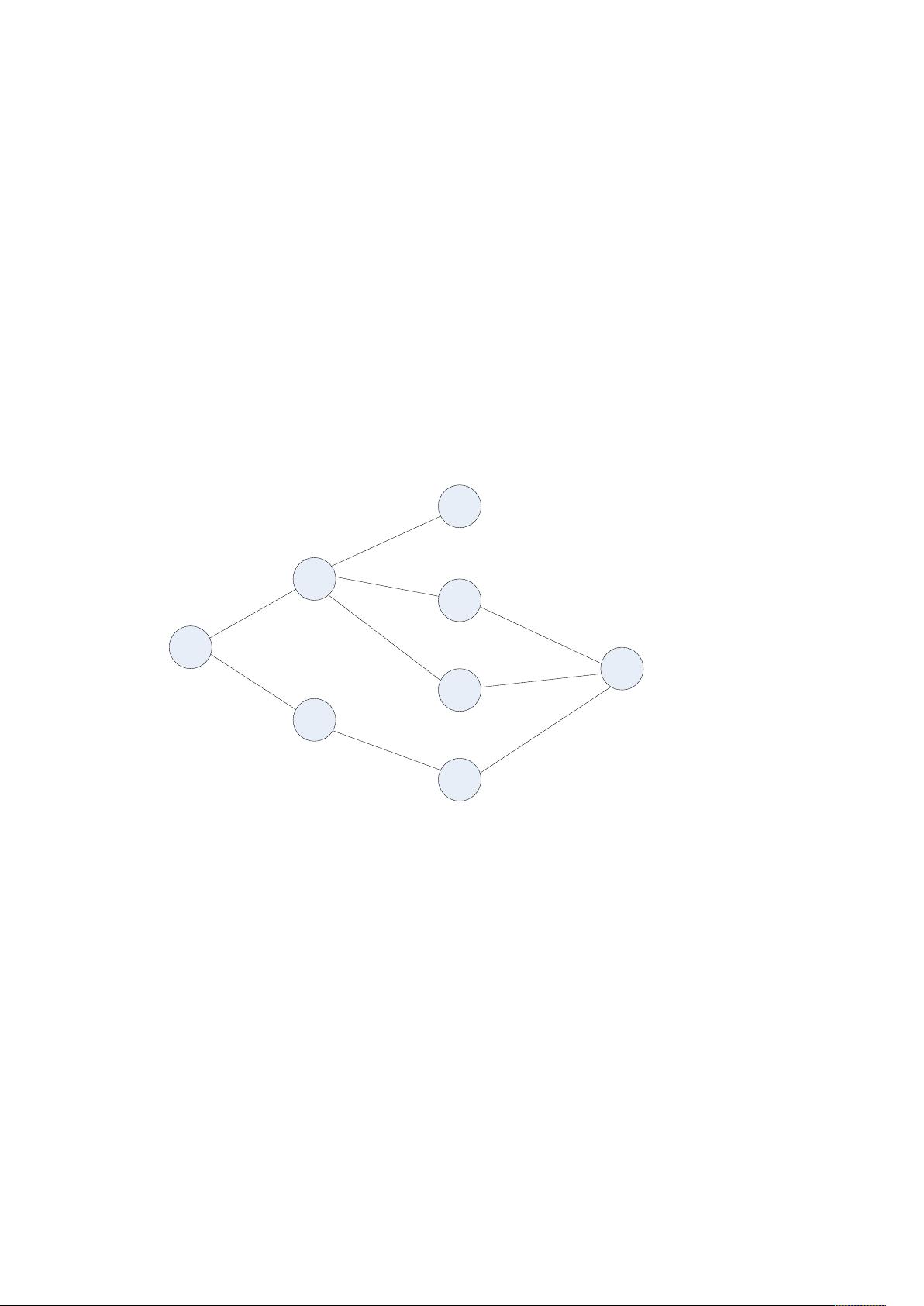
无向连通图两点间所有路径的Java算法实现

"该资源提供了一个使用Java描述的算法，用于找出无向连通图中两点之间所有不包含环路或重复节点的路径。" 在无向连通图中，寻找两点之间的所有路径是一个常见的图论问题。这个问题可以通过深度优先搜索（DFS）或者广度优先搜索（BFS）的方法来解决，这里采用的是基于DFS的递归方法。以下是算法的详细解释： 1. **构建节点关系**：首先，我们需要构建图的结构。每个节点代表图中的一个顶点，节点内部有一个集合存储与其直接相连的所有其他节点（不包括自身）。这样，我们可以快速地找到与一个节点相邻的所有节点，这对于执行后续的路径搜索至关重要。 2. **定义递归子问题**：从起始节点开始，我们将问题分解为求解每个相邻节点到终点的所有路径。每次递归调用，我们都会选择一个相邻节点，并在其基础上寻找到达终点的路径。例如，如果我们要找从A到H的所有路径，可以将问题转化为找到B到H和C到H的所有路径，然后将结果合并。 3. **使用栈进行回溯**：栈在这里用于保存在寻找路径过程中遇到的节点。每当找到一个完整路径时，我们会将栈顶节点弹出，因为它已经完成了其作用。当遇到无法继续向下搜索的情况（即没有与栈顶节点相连的节点可以到达终点），也需要弹出栈顶节点以回溯到前一个节点，尝试其他的分支。 4. **算法伪码**： ```java public class Main { Stack<Node> stack = new Stack<>(); // 临时保存路径节点的栈 ArrayList<String> paths = new ArrayList<>(); // 存储路径的集合 public static void findPaths(Node start, Node end, String currentPath) { stack.push(start); currentPath += start.getName() + "-"; if (start.equals(end)) { // 如果到达终点，将路径添加到结果列表 paths.add(currentPath.substring(0, currentPath.length() - 1)); // 去掉最后一个分隔符 } else { for (Node neighbor : start.getRelationNodes()) { if (!stack.contains(neighbor)) { // 避免环路 findPaths(neighbor, end, currentPath); } } } stack.pop(); // 回溯 } public static void main(String[] args) { // 初始化节点和边，调用findPaths方法 } } public class Node { // ... （节点属性和方法） } ``` 上述代码展示了算法的基本框架。`findPaths`方法是递归的核心，它接受起始节点、结束节点和当前路径作为参数。`main`方法中需要初始化图的节点和边，并调用`findPaths`方法开始搜索。 5. **防止环路**：在递归过程中，通过检查栈中是否已存在当前要访问的节点，可以避免进入环路。如果栈中包含当前节点，说明之前已经访问过这条路径的一部分，因此跳过该节点的进一步搜索。 6. **处理重复节点**：由于题目要求路径上不能有重复的节点，所以在路径字符串`currentPath`中记录节点，可以确保在合并路径时不会包含重复的节点。 通过这个算法，我们可以有效地找出无向连通图中两点间的全部路径，同时避免了环路和重复节点的出现。这在图算法中有着广泛的应用，比如在网络路由、数据结构分析等领域。