着色算法驱动的程序分析与8寄存器优化详解

本篇文档主要探讨了程序分析与优化中的一个重要环节——寄存器分配。在程序设计中，寄存器分配是一项关键任务，涉及到为程序中的变量选择合适的存储位置，即决定是将其存储在速度快但数量有限的寄存器中，还是速度较慢但容量巨大的内存中。这一过程需要考虑寄存器的使用策略，如寄存器指派、溢出处理以及寄存器合并。 8.1.1 寄存器分配的核心工作 寄存器分配主要包括两部分：寄存器指派，即将变量分配到物理寄存器；以及寄存器溢出处理，当一个变量的使用频率超过可用寄存器时，需要考虑如何有效地共享或重用寄存器。同时，编译器还需要遵循调用约定（calling convention），确保同一程序点上活跃的多个变量被分配到不同的寄存器。 8.1.2 寄存器约束 有些变量可能受到硬件限制或编程约定的影响，必须存放在特定的寄存器中。此外，虚拟寄存器（程序中的变量）和物理寄存器（硬件实际的寄存器）之间也存在映射关系。程序执行中，同一个变量在不同分支中的使用必须保持一致性，以避免后续处理中的数据混乱。 8.1.3 寄存器分配与生命周期管理 在优化过程中，算法需要确保最小的寄存器数量能满足最长生命周期变量的需求。然而，例如在DCC888课程中的例子，尽管MaxLive（最长生存期）是2，但MinReg（最小寄存器数量）需要3，这是因为考虑到分支的处理。如果每个分支使用不同的寄存器，会在汇聚点导致额外的转移操作，这会增加寄存器需求或引入更多指令，从而增加开销。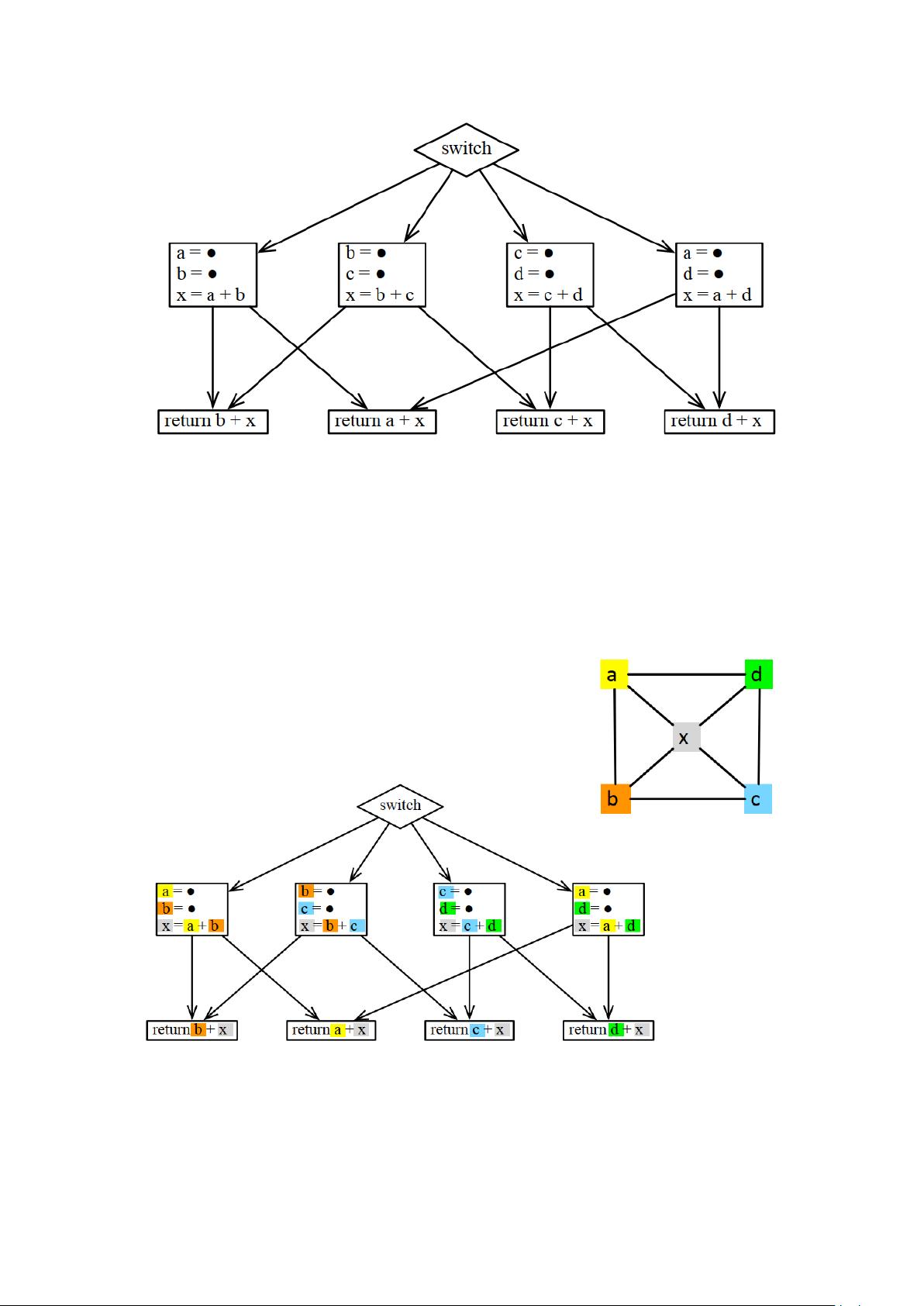 8.1.4 寄存器分配的复杂性与NP问题 寄存器分配是一个典型的NP完全问题，其复杂度与图的着色问题相当。解决策略需要寻找最少颜色（寄存器数量）来满足特定的变量使用规则。在复杂的控制流图（CFG）中，确保同一变量在多个分支的汇聚点上使用相同的寄存器是着色问题的关键。 8.2 线性扫描算法 线性扫描是一种基于区间图的贪婪着色算法，用于寻找最少颜色的寄存器分配。虽然它不是贪婪着色的最优解，但提供了近似最优的结果。算法首先对基本块（BB）进行线性化，通常是通过逆后根排序来排列，这与程序执行顺序密切相关。 8.2.2 区间线生成 变量的区间线定义为该变量从出生到死亡期间活动的所有程序点。例如，变量b和e的区间线会延伸到第二个基本块的末尾，因为后续可能存在依赖，直到它们的生命期结束或分支条件不再涉及。 总结，寄存器分配是程序优化的重要步骤，它涉及到策略选择、约束处理和复杂问题求解。通过理解这些概念，开发者可以更好地优化代码性能，尤其是在处理多分支和复杂控制流的程序时。