机器学习中的距离与相似度度量：欧式、曼哈顿、切比雪夫与闵可夫斯基

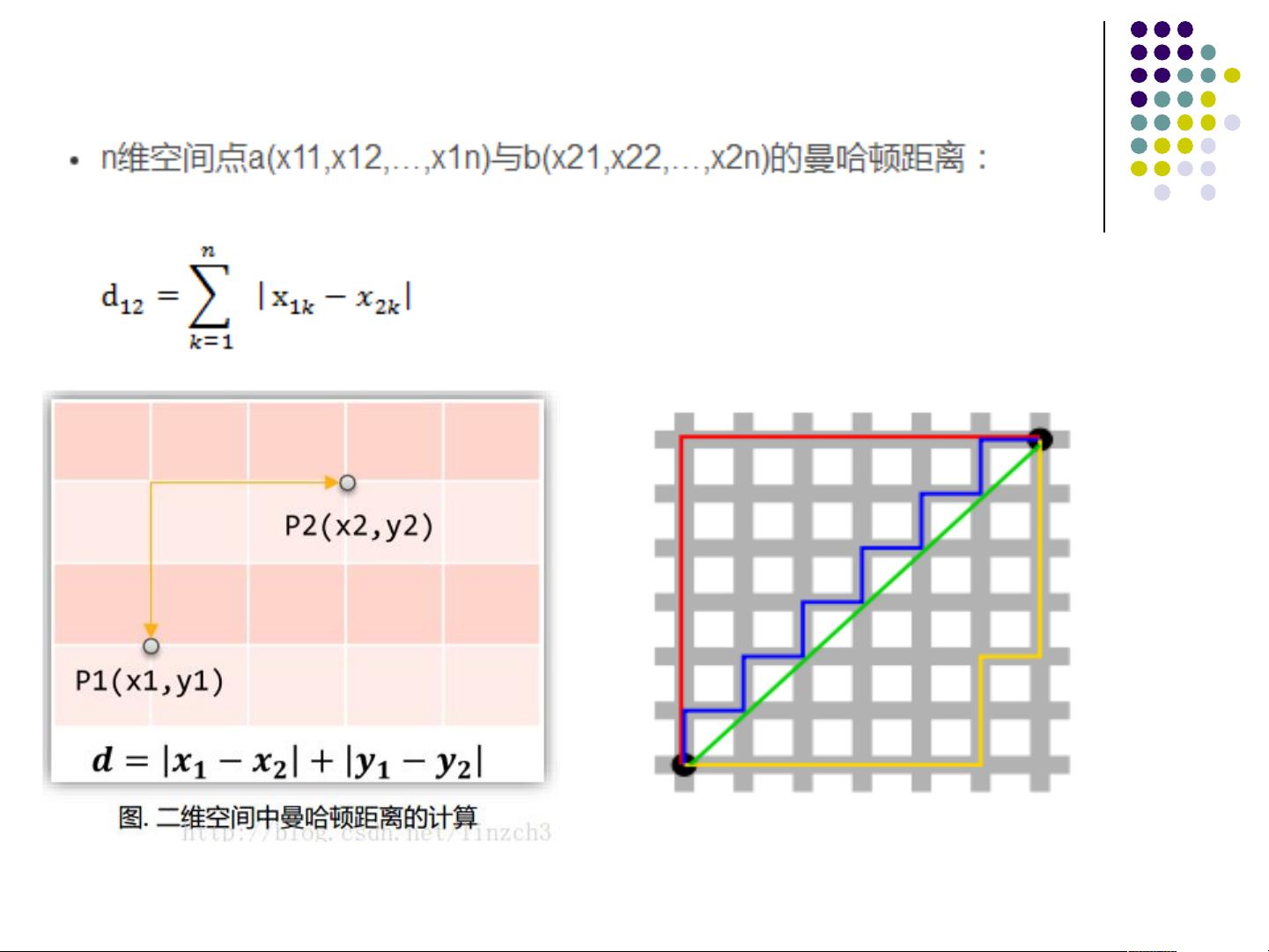
"此资源是一个关于机器学习中距离与相似度度量的PPT总结，涵盖了多种计算方法，如欧式距离、曼哈顿距离、切比雪夫距离和闵可夫斯基距离，并讨论了它们的适用场景和潜在问题。" 在机器学习领域，距离和相似度度量是至关重要的概念，它们帮助我们量化数据点之间的差异，从而进行分类、聚类和其他分析任务。下面我们将详细探讨这些度量方法。 1. 欧式距离：这是最直观的距离度量，由两点在所有维度上差值的平方和的平方根计算得出。适用于数据在各个维度上有相同量纲的情况。然而，如果不同维度的尺度差异较大，欧式距离可能会失真，因为较大的差异会被放大。 2. 曼哈顿距离：也被称为城市街区距离，是各个维度差值的绝对值之和。它不考虑维度之间的相对大小，而是简单地累加每个维度上的距离。在数据具有独立的、非连续的特征时，曼哈顿距离可能是合适的。 3. 切比雪夫距离：最大坐标差值，即两个点在任一维度上的差值的最大值。在某些情况下，如当我们需要关注最大偏离时，例如在棋盘移动问题中，切比雪夫距离特别有用。 4. 闵可夫斯基距离：这是一个通用的距离度量公式，包括了欧式距离和曼哈顿距离作为特殊情况。通过调整参数p，我们可以得到不同类型的度量。当p=2时，我们得到欧式距离；当p=1时，我们得到曼哈顿距离；当p趋向无穷大时，我们接近切比雪夫距离。这个度量允许我们灵活地处理不同重要性的特征，但同样面临量纲和分布问题。 然而，上述距离度量存在一些共同的缺点。首先，它们通常假设所有特征在同一尺度上，这可能导致某些特征的影响力过大。其次，它们可能忽略了特征的分布差异，如高斯分布和均匀分布的特征可能需要不同的处理方式。为了解决这些问题，常常会进行标准化，如Z-score标准化，使得所有特征的均值为0，标准差为1，这样可以消除量纲影响并平衡各特征的权重。 此外，还有其他度量，如余弦相似度，它基于两个向量的夹角，而非它们的长度，因此不受特征尺度的影响。还有Jaccard相似度，适用于比较集合的相似性，如文本中的关键词出现情况。 在实际应用中，选择哪种距离度量取决于具体问题和数据特性。对于多维数据，主成分分析(PCA) 或其他降维技术可以帮助识别重要特征并减少维度影响。同时，使用核方法如支持向量机(SVM)也可以间接地处理非线性关系和特征尺度问题。 理解和选择适当的距离与相似度度量是机器学习中关键的一步，它直接影响模型的性能和解释性。在实践中，可能需要尝试多种度量方法，结合业务理解，找到最适合问题的解决方案。