EM算法Python实现与解析：双硬币问题解决步骤

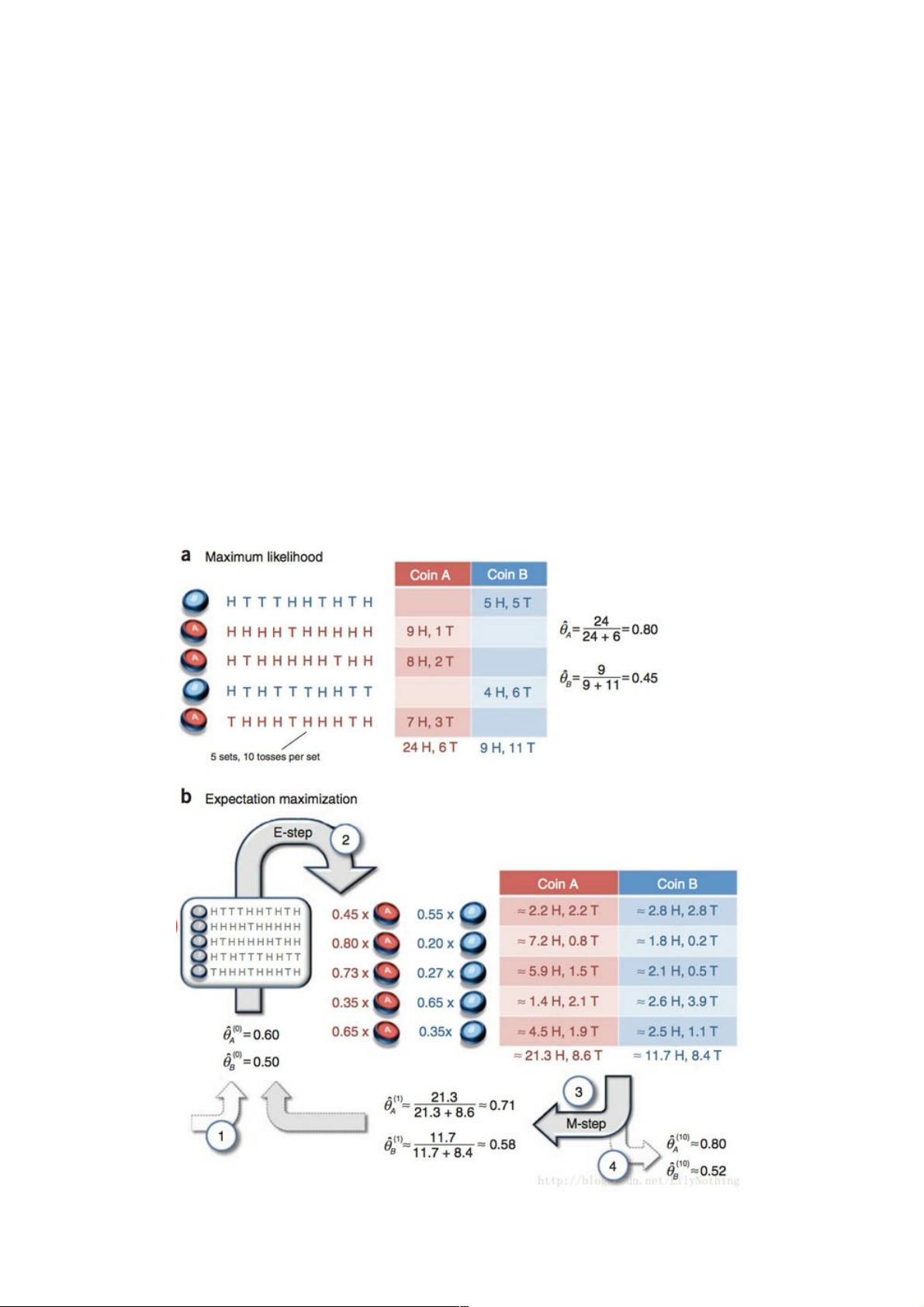
"本文主要介绍EM算法的Python实现，通过双硬币问题来阐述EM算法在处理含有隐变量问题中的应用。" EM算法（Expectation-Maximization，期望-最大化）是一种用于估计统计模型参数的迭代方法，尤其适用于含有隐变量的概率模型。在双硬币问题中，我们有两个硬币A和B，它们有不同的正面朝上的概率，但观察数据可能不包含硬币的选择信息。EM算法在这种情况下能够帮助我们估计每个硬币的正面出现概率。 首先，我们需要构建观测数据集，这里以0表示反面，1表示正面，创建一个二维数组来表示5次实验的10次投掷结果。 接着，我们进行EM算法的初始化阶段，给硬币A和B的正面概率（θ_A 和 θ_B）赋初值，通常选择随机值或均匀分布。 在EM算法的E步骤（期望步骤）中，我们需要计算每个观测值属于硬币A的概率（责任分配）。这里可以利用二项分布的累积密度函数（CDF）或概率质量函数（PMF），如`scipy.stats.binom.pmf`来计算。对于第一行数据，我们计算每种情况（即每个硬币）下出现当前观测结果的概率。 在M步骤（最大化步骤）中，我们将更新硬币的参数。基于E步骤得到的责任分配，我们重新估计每个硬币的正面概率。这通常涉及到对所有观测值的加权平均，权重是E步骤计算出的概率。 算法会重复E步骤和M步骤，直到参数收敛或者达到预设的最大迭代次数。每次迭代都会使似然函数增加，直至找到局部最优解。 在双硬币问题中，EM算法能够处理实习生未记录硬币选择这一隐变量的情况，从而有效地估计出每个硬币的正面概率。通过不断迭代，我们可以逐步接近真实的硬币概率，即使在数据中没有直接提供硬币选择信息的情况下。 EM算法是解决含有隐变量问题的一种强大工具，它在机器学习、自然语言处理和生物信息学等领域有广泛应用。Python中的实现可以通过科学计算库如NumPy和SciPy来辅助，使得复杂概率模型的参数估计变得相对简单。