量子概率：从复数到认知现象的探索

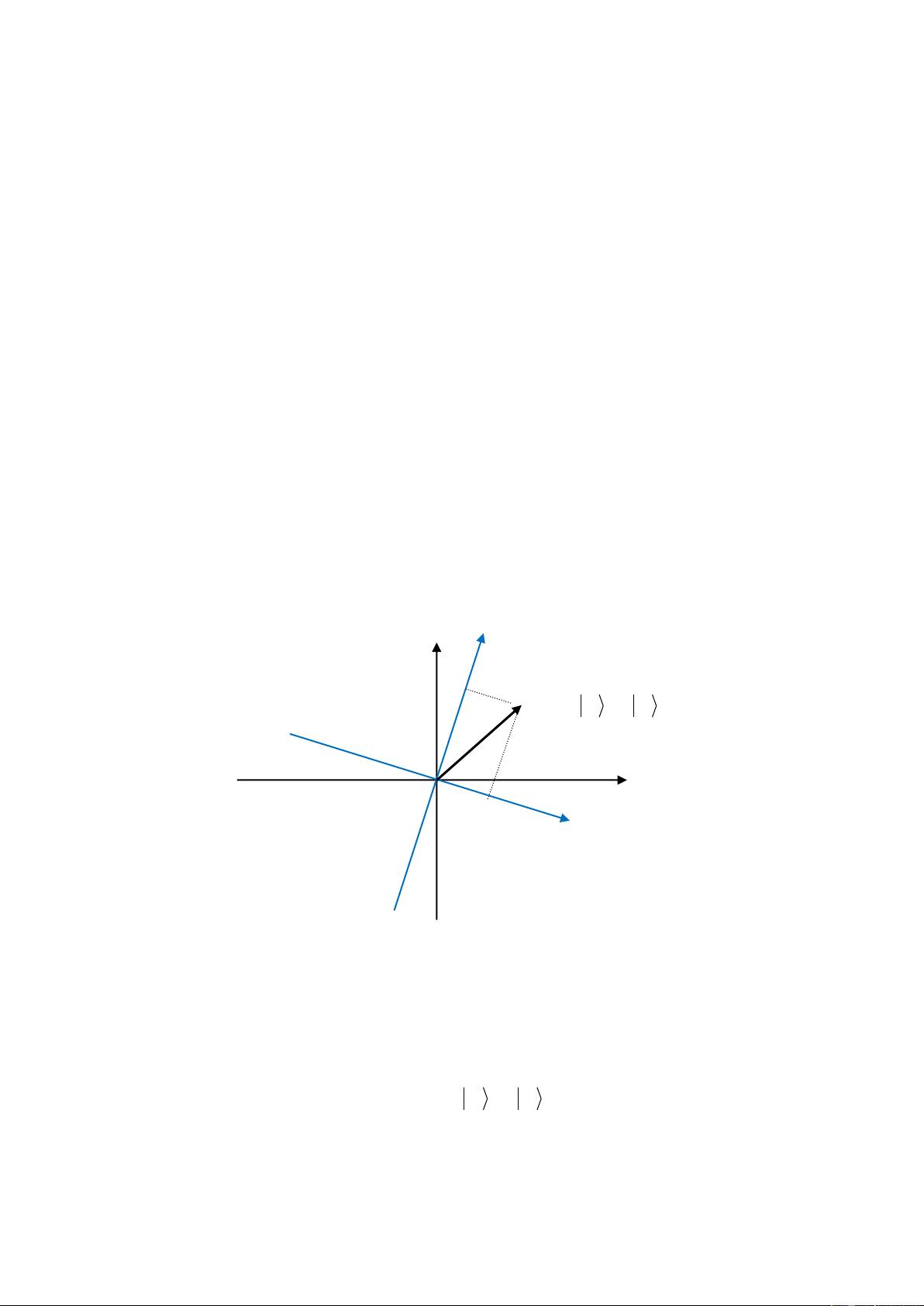
"这篇文档是关于量子概率的简介，作者张江探讨了量子概率作为数学概念，不仅限于描述微观粒子，也可应用于宏观系统，如人类认知现象。文章通过复数概率的角度，揭示了量子概率如何扩展经典概率，并强调了观察者在不确定性中的角色。文中涉及复数概率的概念、不兼容属性对、复合系统、纠缠态和贝尔不等式，旨在展现量子概率与经典概率的差异。最后，作者简要介绍了量子概率在人类认知现象中的应用，以及对不兼容属性对、纠缠和贝尔不等式的拓广讨论。" 量子概率是源自量子力学的一种数学工具，它超越了传统物理学的范畴，不再仅仅关注物质世界，而是关注符号之间的关系和结构。在这个框架下，概率可以是复数，而不仅仅是经典的0到1之间的实数。复数概率，或称概率幅，引入了虚部，使得概率理论有了更丰富的表达能力。 复数概率在处理不确定性时具有更深层次的意义。经典概率描述的是事件发生的可能性，而量子概率则考虑到了观测过程本身对系统状态的影响，以及观察者的信息处理能力限制。这导致量子概率中的不确定性更加复杂，因为它们包含了观测过程的相互作用和信息处理的局限。 文章逐步引导读者理解这一概念，从复数概率幅出发，讨论了不兼容属性对（即无法同时精确测量的物理量，如位置和动量），这些属性在量子系统中表现出非经典的关联。接着，作者深入到复合系统和纠缠态，纠缠是量子力学中的一个关键特征，描述了两个或多个粒子间的状态无法独立描述，即使它们相隔很远，一个粒子的状态改变会瞬间影响到另一个。 贝尔不等式是经典概率与量子概率差异的有力证据，它在量子世界中可能会被违反，这表明量子系统的性质超出了局部隐变量理论的预期。文章中对贝尔不等式的讨论，进一步揭示了量子概率的非局域性和非经典特性。 最后，作者讨论了量子概率在人类认知领域的应用，提出了将认知主体视为量子系统的一种方式，利用量子概率描述观察者对外界信息的处理和理解。这种应用并不意味着将认知过程简化为微观粒子的运动，而是整体地看待认知系统，考虑其内在的不确定性。 总结来说，这篇文档深入浅出地介绍了量子概率的概念和其与经典概率的差异，以及它在不同领域，尤其是人类认知科学中的潜在应用。通过复数概率的视角，读者可以更全面地理解量子世界的奇异性和复杂性。