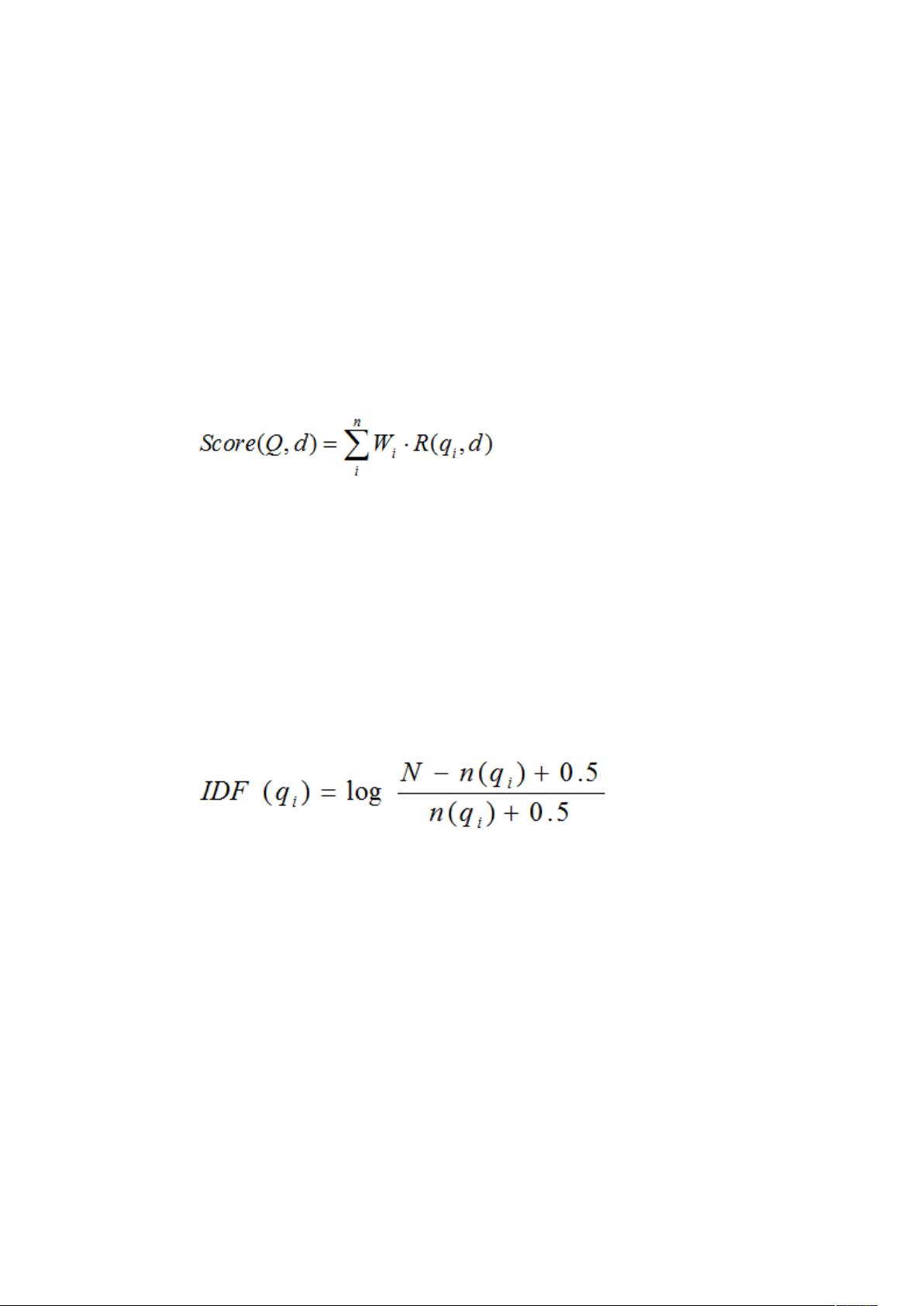BM25算法详解：搜索相关性评分的关键技术

"BM25算法是一种用于信息检索和搜索引擎中的相关性排名算法。它基于文档的词频和逆文档频率（IDF）来评估查询（Query）与文档（Document）之间的相关性。该算法考虑了词频、文档长度和其他调整因子，以提供更准确的搜索结果排序。" 在BM25算法中，每个查询词被分解成语素，并对每个搜索结果文档计算这些语素的相关性分数。这些分数随后被加权求和，得出整个查询与文档的相关性总分。公式表达如下： \[ \text{score}(Q, d) = \sum_{i=1}^{m} \frac{f_{qi} \cdot (k_1 + 1)}{f_{qi} + k_1 \cdot (1 - b + b \cdot \frac{\text{dl}}{\text{avgdl}})} \cdot \text{IDF}(qi) \] 其中： - \( Q \) 表示查询， - \( qi \) 是查询中的第 \( i \) 个语素， - \( d \) 是一个文档， - \( f_{qi} \) 是语素 \( qi \) 在文档 \( d \) 中的频率， - \( k_1 \) 和 \( b \) 是常数调节因子，通常 \( k_1 = 2 \)，\( b = 0.75 \)， - \( \text{dl} \) 是文档 \( d \) 的长度， - \( \text{avgdl} \) 是所有文档的平均长度， - \( \text{IDF}(qi) \) 是语素 \( qi \) 的逆文档频率，计算公式为 \( \text{IDF}(qi) = \log{\frac{N}{n(qi) + 1}} \)，其中 \( N \) 是索引中所有文档的数量，\( n(qi) \) 是包含语素 \( qi \) 的文档数。 IDF反映了语素的稀有性，一个在较少文档中出现的语素具有更高的IDF值，表明其在区分文档方面更有效。 在计算相关性得分时，\( K \) 的定义考虑了文档长度的影响。较长的文档可能会有更高的词频，但为了防止长文档总是获得较高的得分，引入了 \( b \) 参数来调整这种影响。较小的 \( b \) 值会使文档长度的影响减小，而较大的 \( b \) 值则会增强长度的影响。 BM25算法的优势在于其灵活性，可以通过选择不同的语素分析方法、语素权重计算方式（如TF-IDF）以及文档相关性评估方法来适应不同的场景。此外，通过调整 \( k_1 \) 和 \( b \) 参数，可以根据具体应用的需求来优化算法性能。 BM25算法是现代搜索引擎中广泛应用的一种技术，它通过综合考虑词频、文档长度和词的全局分布，提供了一种衡量查询与文档之间相关性的量化方法。这种算法的灵活性和准确性使其成为文本检索领域的一个重要工具。