卡尔曼滤波：解决传感器误差与估计值融合的优化算法

本文主要讲解卡尔曼滤波（Kalman Filter）及其在解决存在误差的传感器数据融合问题中的应用。卡尔曼滤波是一种数学模型，广泛应用于诸如自动驾驶、无人机导航、信号处理等领域，尤其对于处理高维动态系统的状态估计非常有效。 在实际应用中，如温度计示数偏差问题，卡尔曼滤波提供了一种动态调整权重的方法，使得系统能够自动根据传感器观测值和内部估计的不确定性来实时更新状态。相比于传统的互补滤波，卡尔曼滤波更为智能，因为它会根据时间序列数据自适应地调整权值，无需人为设定固定权重，从而提高估计的准确性。 为了理解卡尔曼滤波，先要掌握一些基础知识： 1. **高斯分布**：也称为正态分布，是描述随机变量概率分布的一种重要工具，常用于刻画传感器读数的不确定性。理解高斯分布有助于构建卡尔曼滤波中的概率模型。 2. **方差与协方差**：方差是衡量数据波动性的指标，而协方差则反映两个变量变化的一致性。在卡尔曼滤波中，方差用于量化观测噪声的大小，协方差则用于计算状态变量之间的依赖关系。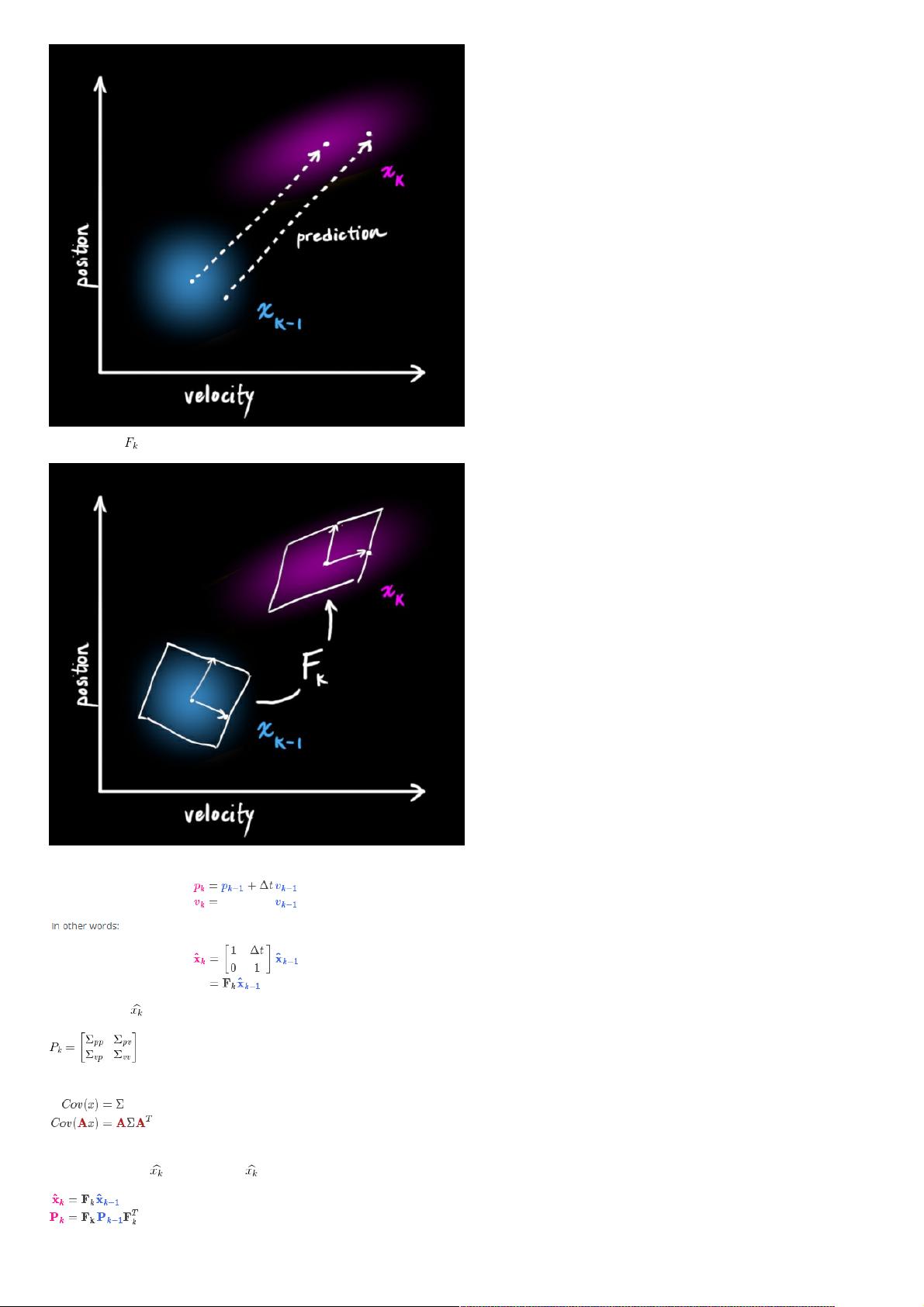 在卡尔曼滤波的具体步骤中，主要包括以下几个关键环节： - **预测（Prediction）**：根据上一时刻的状态和运动模型，预测下一时刻的状态，同时更新状态的协方差矩阵。 - **更新（Update）**：利用当前观测值与预测值的差异，通过卡尔曼增益来调整预测值，得到新的状态估计，并更新协方差矩阵。 对于小机器人导航的例子，其状态变量包括位置(p)和速度(v)，这两个变量都是向量，且可能受到噪声的影响。卡尔曼滤波器将对这些状态变量进行持续的估计和更新，确保机器人的导航路径尽可能接近真实状态。 代码部分可能包含卡尔曼滤波器的实现细节，如使用递推公式（EKF，Extended Kalman Filter的扩展版本），初始化矩阵，以及在线更新过程中的计算。学习和实现卡尔曼滤波不仅需要掌握数学理论，还需理解如何将其应用于特定的控制系统和硬件环境中。 总结来说，卡尔曼滤波是一个强大的工具，通过结合概率统计和动态系统的知识，能够在不断变化的环境中提供更精确的状态估计，这对于依赖传感器数据的现代技术系统至关重要。通过本文提供的理论和代码示例，读者可以深入了解卡尔曼滤波的工作原理，并尝试将其应用到实际问题中。