探索四元数与三维旋转的直观几何关联

本文主要探讨了三维旋转与四元数之间的联系，特别是针对计算机图形学和工程领域中对这种数学工具在处理三维空间变换的应用。四元数是一种扩展的复数形式，用于表示三维空间中的旋转，相比于传统的旋转矩阵，它具有更高的效率和便利性。 首先，文章从复数的基本概念出发，指出复数可以表示为实部和虚部的组合，且虚数单位满足\( i^2 = -1 \)。通过将复数看作是向量在特定基（Basis）上的线性组合，作者引入复数与二维旋转的关联，为理解四元数奠定了基础。四元数实际上是复数的扩展，由四个实数构成，包含了一个额外的虚数分量，使得它可以同时表示三维空间中的三个旋转轴和一个旋转角度。 在介绍四元数时，作者强调许多四元数的性质与复数相似，这有助于读者通过已有的复数知识来逐步掌握四元数。四元数的表示形式通常为 \( q = w + xi + yj + zk \)，其中 \( w \) 是实部，而 \( x, y, z \) 分别对应三个旋转轴上的分量，其乘法规则与复数不同，但直观上反映了旋转的组合特性。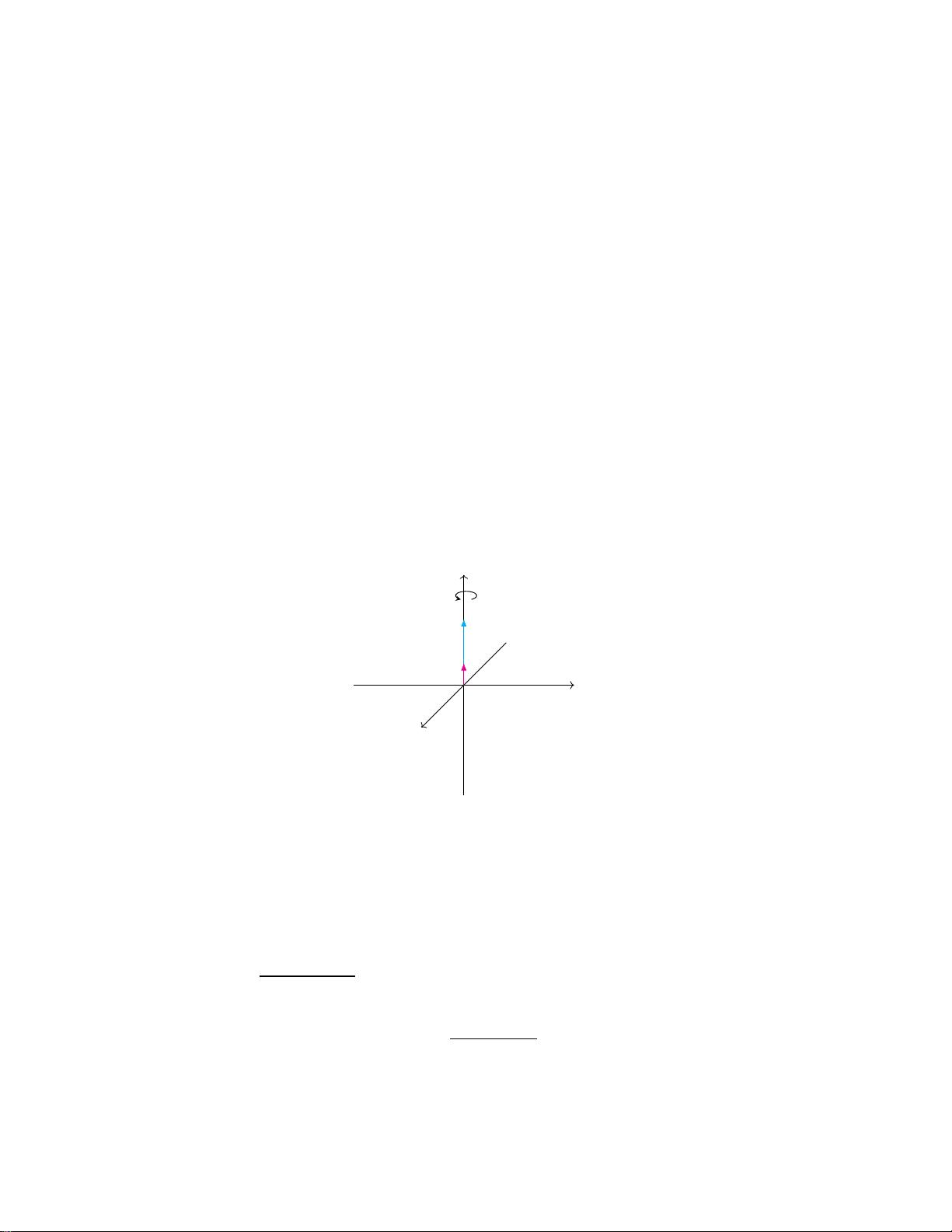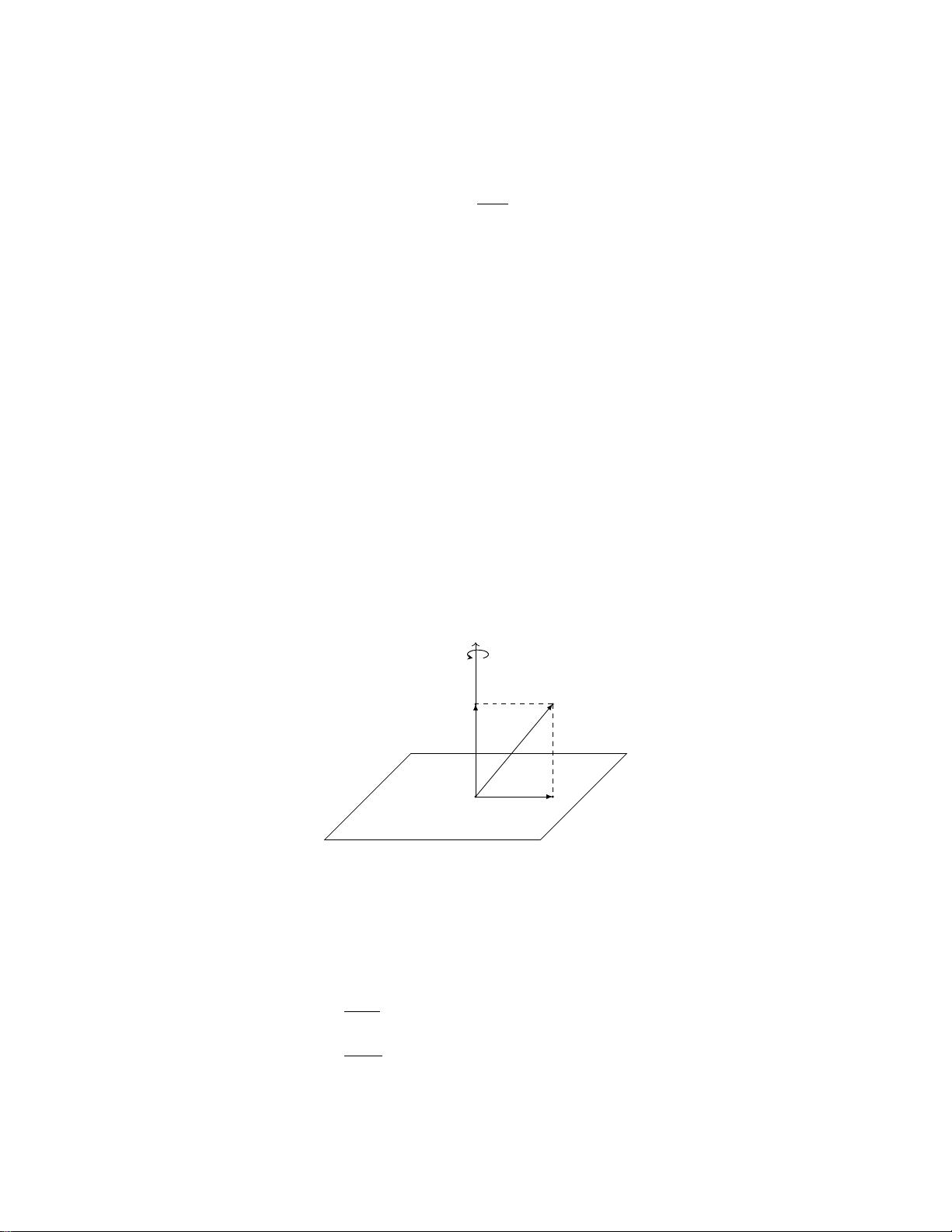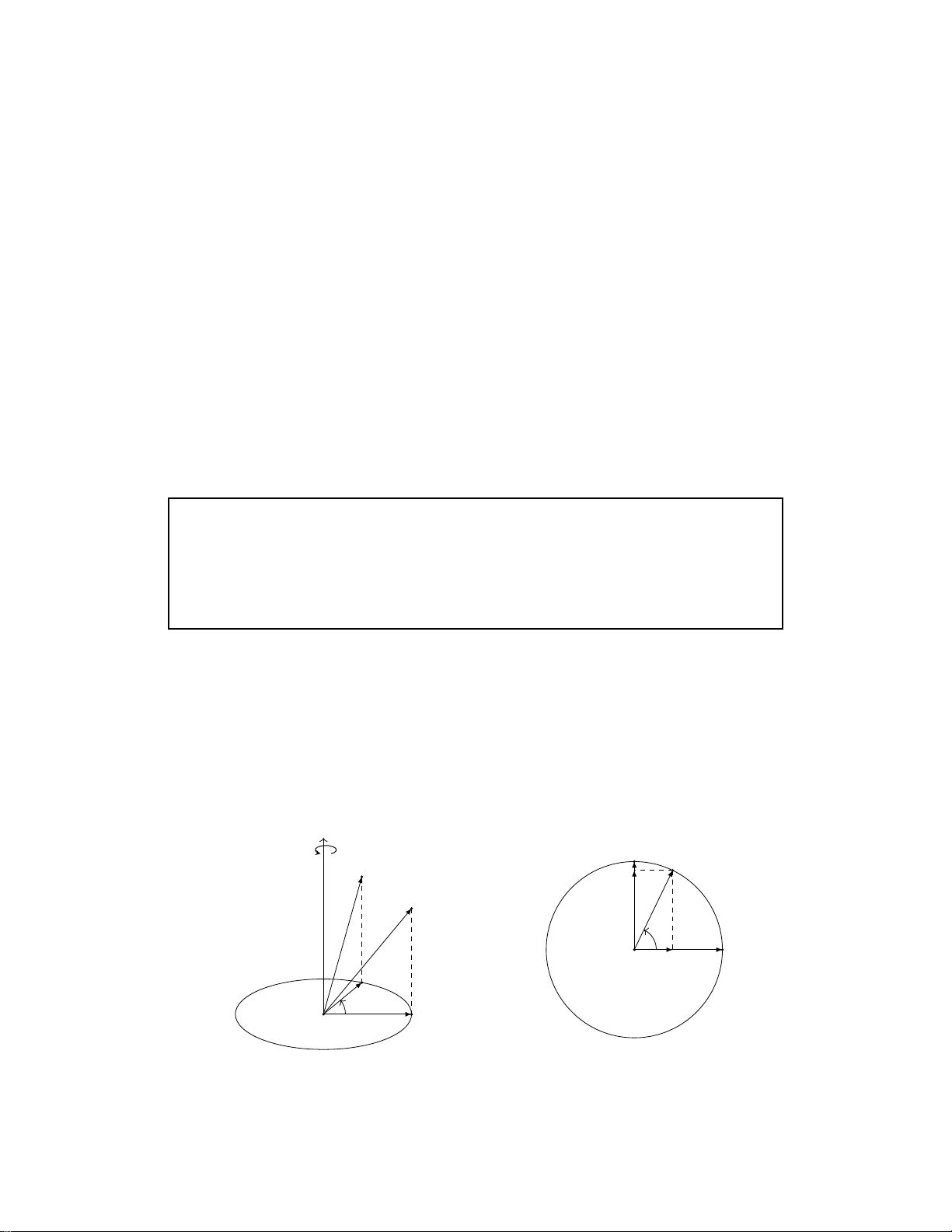 文章指出，四元数与三维旋转的关系可以通过几何方法和线性代数进行直观理解，而不是完全依赖于抽象的代数表达。这对于实际工程应用来说更为实用，例如在飞行控制（飞控）中，四元数常用于高效地表示和计算飞行器的姿态变化。 作者还分享了自己编写的MATLAB/Octave代码示例和相关的GitHub链接，供读者进行实践和验证。此外，他还提醒读者，尽管文章主要关注几何和应用层面，对于那些更侧重理论背景的读者，文章可能不是最佳选择，但最后的拓展阅读部分可能会提供一些参考价值。 文章在撰写过程中可能存在一些错误，作者鼓励读者提出反馈，以便不断改进。同时，作者声明了文章的版权信息，希望在共享和引用时遵循相应的许可协议，且避免商业用途。 这篇文档为初学者和专业人士提供了一个简明易懂的桥梁，帮助他们理解四元数如何与三维旋转无缝结合，特别是在计算机图形学和工程实践中如何有效地利用这一工具。