深度解析：支持向量机：理论与应用

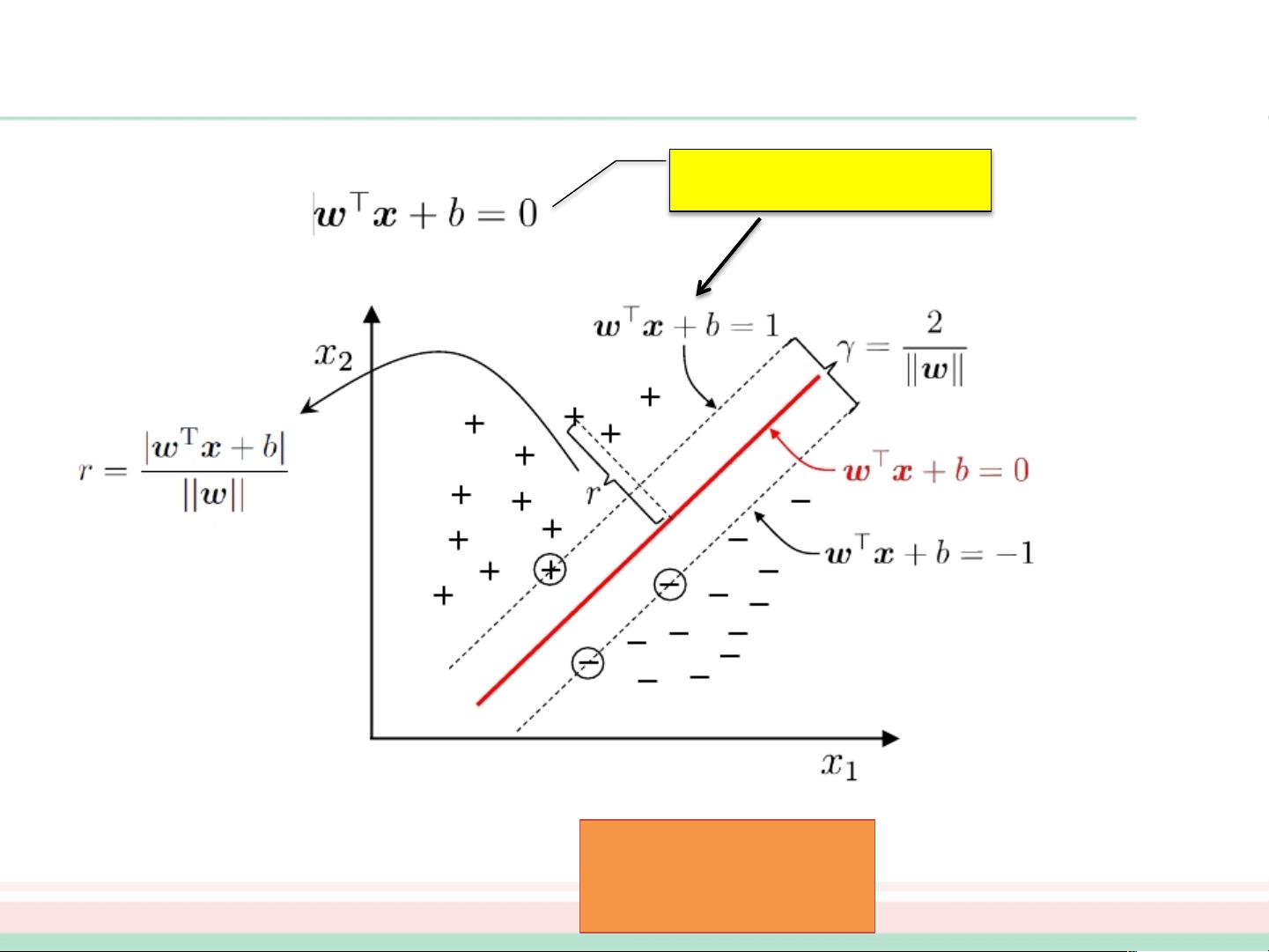
支持向量机(SVM)是一种强大的分类算法，在现代机器学习中占有重要地位。它源自统计学理论，尤其适用于高维数据，因为它能有效地处理维度灾难问题，即随着特征数量增加，数据复杂度并不会急剧增长。SVM的核心概念包括超平面和间隔（margin）。 超平面是线性分类器的基础，它是判定不同类别样本的决策边界。如果g(x)是线性的，那么这个平面就是超平面，其法向量w决定了分类方向。选择最佳超平面的目标是在尽可能保证所有样本点到决策边界的距离（间隔）的同时，使得模型具有良好的鲁棒性和泛化能力。在众多可能的超平面中，位于两类训练样本中心的超平面被认为是最好的，因为它对训练集外的数据有较强的抵抗误差的能力。 支持向量是那些最靠近超平面的样本点，它们的存在确保了最大的间隔。这些样本点的重要性在于，它们使得超平面的定义（wTxi+b=0）变为等于正或负一，这就意味着即使有噪声或者异常值，只要这些支持向量的位置不变，分类性能就不会受到影响。在理想情况下，支持向量到超平面的距离等于间隔，它们是确定分类模型的关键部分。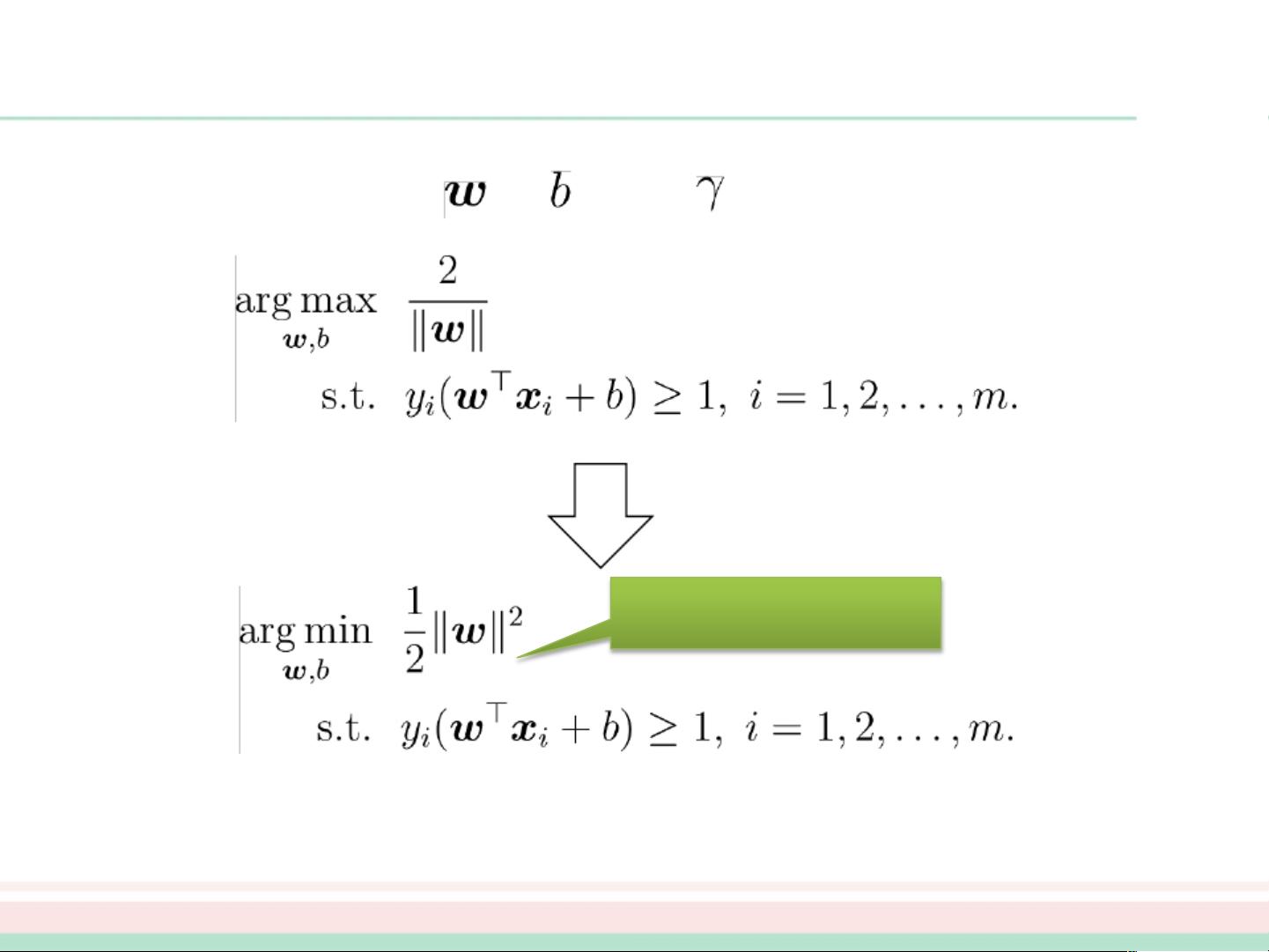 SVM的优化目标是找到这样的超平面，使得支持向量到其对应类别的边界距离最大，这个距离就是间隔。通过最大化间隔，SVM能够形成一个稳定的模型，对于新的输入数据，即使有噪声，也能保持较好的分类性能。此外，SVM中的w和b参数是可以等价缩放的，这意味着模型并不依赖于它们的具体值，而是取决于它们的方向和大小关系。 支持向量机是一种通过优化间隔来构建分类模型的方法，它的核心是寻找最优的超平面，而这依赖于那些离决策边界最近的支持向量。这种策略使得SVM在面对高维数据和复杂分类问题时表现出色，是机器学习和数据挖掘领域的重要工具。