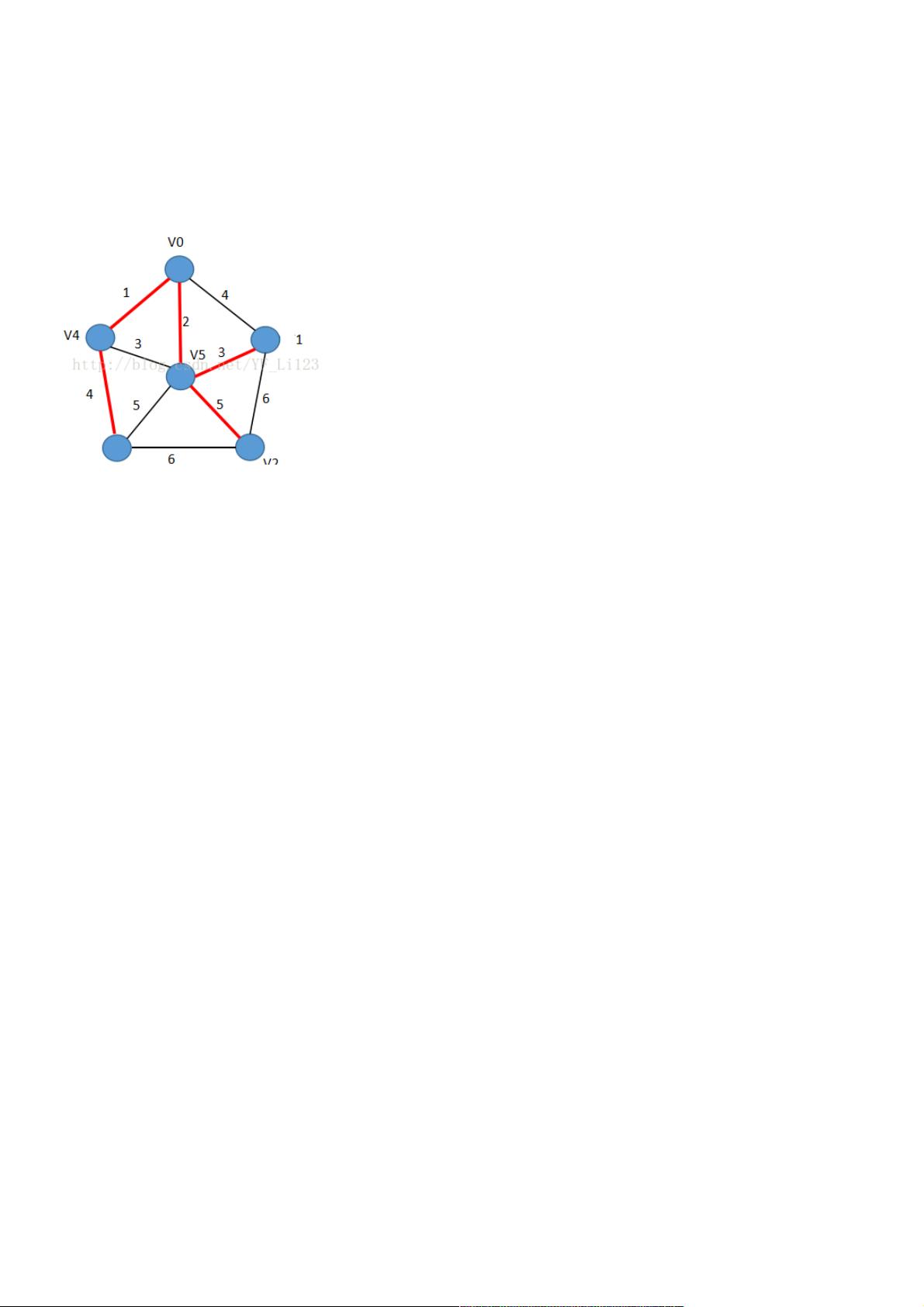
C++实现普里姆算法求最小生成树

最小生成树之普里姆（Prim）算法是一种经典的图论算法，用于在无向图G(V,E)中找到一棵树，该树包含图的所有顶点且边权总和最小。它适用于求解连通带权图的最小生成树问题。Prim算法的核心思想是逐步构建生成树，通过初始化一个集合S，包含起点（通常是任意一个顶点），然后每次从剩余未加入集合的顶点中选择与集合S相连的边中最短的那一条，将连接点添加到集合S，同时更新与新加入顶点相邻节点的距离。 以下是Prim算法的具体步骤： 1. 初始化：设S为一个空集合，V为所有顶点集合，初始时S仅包含一个顶点（例如V0），其余顶点距离设为无穷大（记作INF）。 2. 选择最小边：在V-V（V与V的差集）中找到与S中顶点相连的边中权值最小的一条，这条边的起始端点u被添加到S中。 3. 更新距离：对于S的新成员u，更新它与其他未加入S的顶点v之间的最短距离。这一步可能涉及到邻接矩阵或邻接表的查找操作。 4. 重复步骤2和3，直到S包含所有顶点。此时，S中的边就构成了最小生成树。 值得注意的是，Prim算法的执行过程中不会出现环，因为每次选择的边都是与当前S中顶点相连的最短边，所以生成的树是树形结构。而且，尽管可能存在多个不同的最小生成树，但它们的边权之和总是相同的，这是最小小生成树的特性之一。 在C++实现时，通常会用优先队列（如`std::priority_queue`）来存储未访问的顶点和他们的距离，这样可以在O(log n)的时间复杂度内找到下一个最短距离的顶点，从而提高效率。普里姆算法的时间复杂度为O(E log V)，其中E是边的数量，V是顶点的数量。 最小生成树的普里姆算法是数据结构和算法中的一个重要概念，对于理解和处理实际问题中的网络优化、路由选择等问题具有重要意义。通过C++编程实现，可以帮助我们更好地理解和掌握这一核心算法。