循环重置折现因子EWMA算法：漂移与故障控制

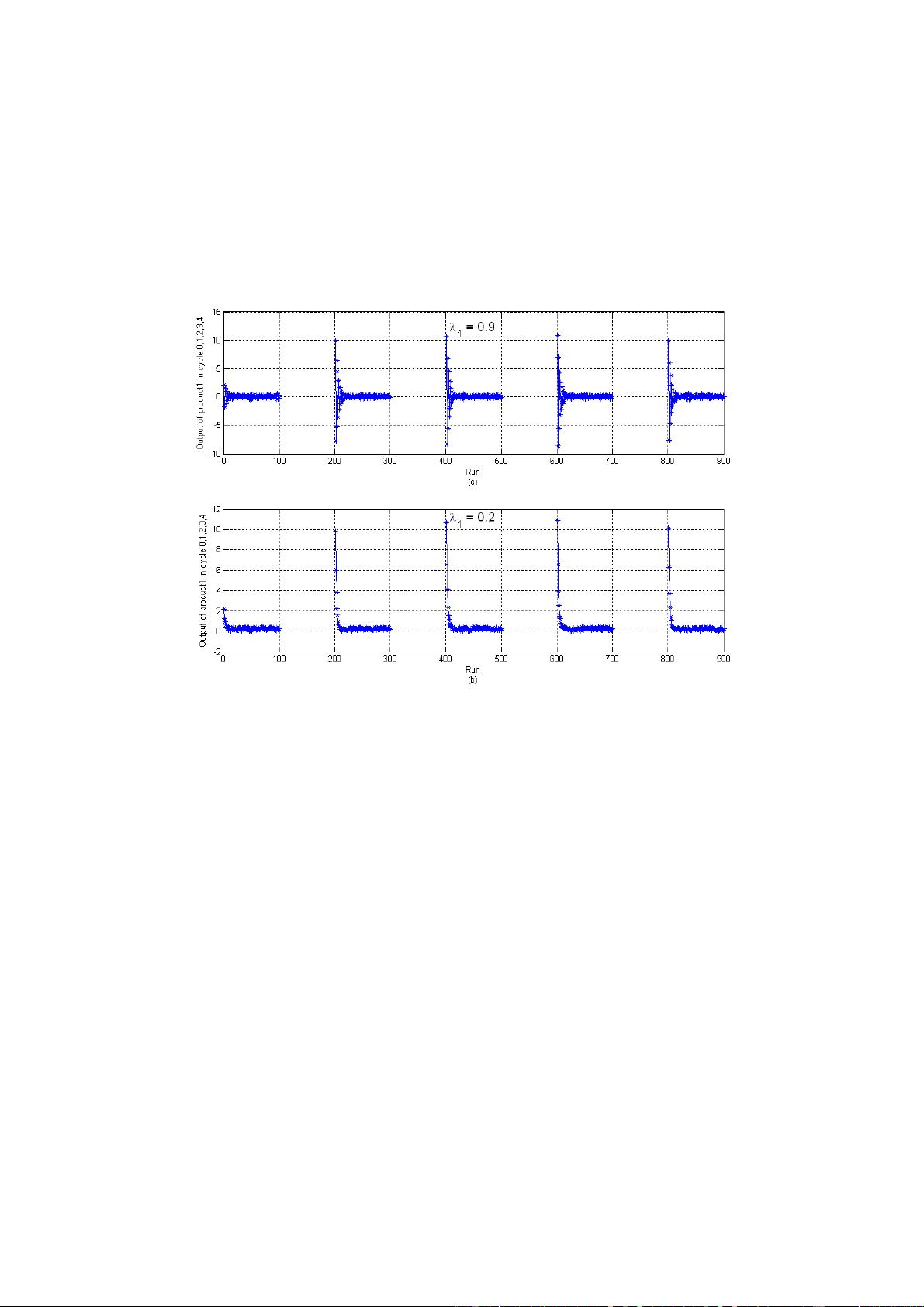
"本文探讨了一种针对高混合运行控制的具有循环重置（CR）折扣因子的指数加权移动平均值（EWMA）算法，旨在解决在半导体制造过程中出现的漂移和故障问题。传统的threaded-EWMA运行到运行控制在面对IMA（1,1）序列干扰和长时间线性漂移时，过程输出可能会出现显著偏差。为了改善这种情况，作者提出了一个循环复位算法，通过引入折现因子来减小这种偏差，从而实现更稳定的控制和最小化渐近方差。此外，文章还研究了如何在系统中集成阶跃故障的处理，通过分析故障宽容（RFT）的方法，以应对可能的故障影响。模拟研究表明，提出的带有CR折扣因子的算法在均方误差（MSE）和方差方面相比固定折扣因子算法减少了约30%至50%，无论过程是否具有振荡，都验证了该方法的有效性。" 在高混合运行控制中，threaded-EWMA算法是关键工具，用于半导体制造工艺步骤的质量控制。然而，当干扰按照IMA（1,1）序列模式发生，伴随确定性的线性漂移和较长的螺纹中断时，控制效果会显著下降。为了克服这一挑战，研究人员引入了具有CR折扣因子的算法。这个CR折扣因子能够在每个周期的早期运行中有效地调整控制策略，以减少由IMA（1,1）序列引起的偏差，从而提高过程的稳定性。 循环重置算法的核心在于动态调整折扣因子，这允许系统在面临漂移或故障时快速适应并校正输出。通过对系统的性能进行深入分析，研究者发现这种动态调整能够显著降低过程的方差，实现更精确的控制。同时，通过故障宽容方法，该算法还能有效地处理阶跃故障，确保即使在故障发生时也能保持控制性能。 通过仿真比较，提出的CR算法在MSE和方差上表现优于固定折扣因子的算法，表明其在处理各种过程动态，尤其是那些包含振荡的复杂过程时，具备更高的控制精度和鲁棒性。这一结果强调了CR算法在实际应用中的潜在价值，尤其是在半导体制造等对精度要求极高的领域。 该研究不仅提出了一种新颖的控制策略，还为高混合运行控制提供了故障容忍能力，为未来的工业应用提供了理论基础和技术支持。通过优化控制算法，可以预期在半导体制造和其他类似流程中，能够实现更高效、更稳定的质量控制。