Python实现平衡二叉树:代码详解与示例
177 浏览量
更新于2024-08-31
收藏 83KB PDF 举报
"本文主要介绍如何使用Python实现平衡二叉树,通过代码示例和理论解释,帮助读者理解平衡二叉树的概念和构建方法。"
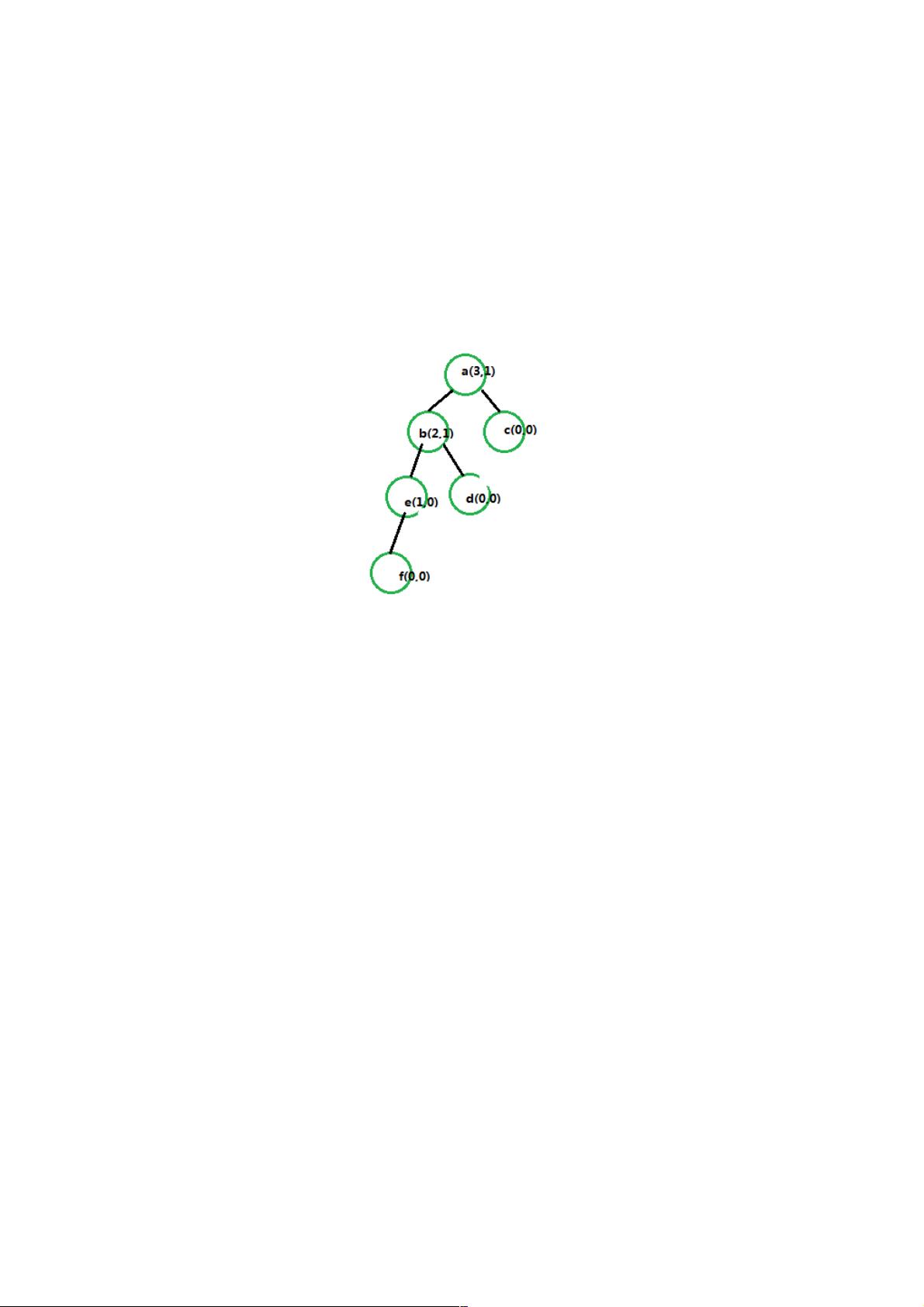
平衡二叉树是一种特殊的二叉树数据结构,它的左右子树的高度差的绝对值不超过1,并且左右子树都是一棵平衡二叉树。这种数据结构对于查找、插入和删除操作具有较高的效率,因为它确保了树的高度相对较小,从而减少了遍历节点的时间复杂度。
在Python中,我们首先需要定义一个节点类(`Node`)来存储节点的值、左右子节点以及它们的高度。接着,我们需要创建一个树类(`tree`),包含根节点、前序遍历、中序遍历和后序遍历的列表,以便进行后续操作。
```python
class Node:
def __init__(self):
self.left_children = None
self.left_height = 0
self.right_children = None
self.right_height = 0
self.value = None
class Tree:
def __init__(self):
self.root = False
self.front_list = []
self.middle_list = []
self.after_list = []
```
构建平衡二叉树的关键在于保持树的平衡状态。当插入新节点导致树失去平衡时,我们需要进行旋转操作来重新平衡树。这里提到了两种旋转方式:左旋和右旋。在示例中,作者提到的是通过调整左偏节点的最右节点来平衡树。不过,实际的平衡二叉树实现通常使用AVL树或红黑树,它们采用更复杂的旋转策略,如单旋、双旋等。
平衡二叉树的插入操作通常包括以下步骤:
1. 插入新节点到二叉树的合适位置。
2. 检查插入操作是否导致树失去平衡。
3. 如果失去平衡,根据失衡类型(左偏或右偏)执行相应的旋转操作。
在Python中,插入操作的伪代码可能如下:
```python
def insert(self, value):
# 创建新节点
new_node = Node(value)
# 插入操作
if not self.root:
self.root = new_node
else:
current_node = self.root
while True:
if value < current_node.value:
if not current_node.left_children:
current_node.left_children = new_node
break
else:
current_node = current_node.left_children
else:
if not current_node.right_children:
current_node.right_children = new_node
break
else:
current_node = current_node.right_children
# 更新节点高度
self._update_height(current_node)
# 检查并平衡树
self._balance(current_node)
def _update_height(self, node):
# 更新节点及其子节点的高度
pass
def _balance(self, node):
# 根据节点的平衡因子判断是否需要旋转,如AVL树的LL、RR、LR、RL旋转
pass
```
实际的`_update_height`和`_balance`函数需要根据具体平衡策略来实现,例如AVL树会计算节点的平衡因子(左右子树高度之差),并根据平衡因子进行相应的旋转操作。在红黑树中,颜色规则和旋转策略则更为复杂。
平衡二叉树是高效数据结构,通过保持树的平衡状态来优化查找、插入和删除操作。Python中的实现需要定义节点和树的类,以及实现插入操作时的平衡调整逻辑。虽然文章中提供的代码示例并不完整,但它提供了一个理解平衡二叉树概念的良好起点。实际编程中,建议参考AVL树或红黑树的标准实现。
641 浏览量
483 浏览量
133 浏览量
109 浏览量
848 浏览量
点击了解资源详情
161 浏览量
2024-12-10 上传
weixin_38694023
- 粉丝: 4
最新资源
- OCP指南:理解价值与分类,避开误区
- Windows 2000 + Oracle 9i 安装配置详指南
- ActionScript 3.0组件使用指南
- C语言指针完全解析:从基础到复杂类型
- Hibernate实战指南:Manning出版社
- 9iClient Form Builder基础开发:安装与环境设置
- Flex与J2EE深度集成:服务导向架构与RIA开发
- Oracle数据库安全:概要文件与用户管理
- Oracle事务管理详解:进程与会话的管控
- Oracle对象管理最佳实践
- Oracle分区管理详解
- Zend Framework入门教程:由Rob Allen撰写
- C语言基础:数据类型详解
- VNC协议详解:登录与桌面共享机制
- SQL入门与实践:基础语句与练习解析
- 《Div+CSS布局大全》网页设计教程